Задача 77667 Найдите значение выражения...
Условие
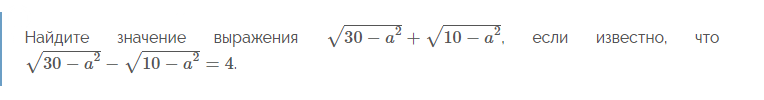
Решение
[m]\sqrt{30–a^2}–\sqrt{10–a^2}=4[/m]
на
[m]\sqrt{30–a^2}+\sqrt{10–a^2}[/m]
получим:
[m](\sqrt{30–a^2}–\sqrt{10–a^2})(\sqrt{30–a^2}+\sqrt{10–a^2})=4(\sqrt{30–a^2}+\sqrt{10–a^2})[/m]
[m] (\sqrt{30–a^2})^2-(\sqrt{10–a^2})^2=4(\sqrt{30–a^2}+\sqrt{10–a^2})=[/m]
[m] (30–a^2)-(10–a^2)=4(\sqrt{30–a^2}+\sqrt{10–a^2})[/m]
[m] 30-10=4(\sqrt{30–a^2}+\sqrt{10–a^2})[/m]
[m] 20=4(\sqrt{30–a^2}+\sqrt{10–a^2})[/m]
[m]\sqrt{30–a^2}+\sqrt{10–a^2}=5[/m]
Все решения
В данном случае разность подкоренных выражений:
[m](\sqrt{30-a^2} - \sqrt{10-a^2})(\sqrt{30-a^2} + \sqrt{10-a^2}) = (30-a^2) - (10-a^2) = 20[/m]
Если известно, что [m]\sqrt{30-a^2} - \sqrt{10-a^2} = 4[/m], то
[m]\sqrt{30-a^2} + \sqrt{10-a^2} = \frac{20}{(\sqrt{30-a^2} - \sqrt{10-a^2})} = \frac{20}{4} = 5[/m]