Задача 77615 Определить, сколько особых точек имеет...
Условие
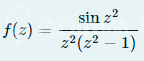
математика ВУЗ
161
Решение
★
[m]f(z)=\frac{sin (z^2)}{z^2(z-1)(z+1)}[/m]
Нули функции f(z) совпадают с нулями числителя этой функции
sin z^2=0 ⇒ z^2= [m]z_{k}=\sqrt{πk}; k[/m] - целое
При [m]k[/m]=0
В точке z_(o)=0 и числитель и знаменатель функции f(z) обращаются в нуль..
Но существует предел
[m]lim_{z → 0}f(z)=lim_{z →0}\frac{sinz^2}{z^2(z^2-1)}=-1/m]
Поэтому
z_(2)=0 -
[i]устранимая особая точка [/i] функции f(z)
Нули знаменателя:
z^2-1=0
z^2=1
z_(1)=-1; z_(2)=1
z_(1)=-1 - [i] полюс первого порядка[/i]
z_(2)=1 - [i] полюс первого порядка[/i]