Задача 77440 ...

6640e3ced6d5273b73493c3f

5/12/2024 3:48:07 PM

e N BN ‘_' @ BN Н э & | £ е° ЕЕ wi § § Ё i LRI R B лН я ака L 2 З ЕО L e ВВ В Ё et 8 В ОЕ B ) S ek o 1Ё Е 88 5 | аОВ ЦЕ аВк В^ : 1ар п ol Е ю- Ё й Е ® ‚ о Ё < . i ' П g . T Т g ® 3 З Е ‹ — 2 8 T g | k) i 4 3 | — &

5f3ea7e3faf909182968ddd9

5/12/2024 4:45:20 PM

★

2sinx*cosx+sinx=cosx+(1/2)

2sinx(cosx+(1/2))=cosx+(1/2)

2sinx(cosx+(1/2))-(cosx+(1/2))=0

(cosx+(1/2))*(2sinx-1)=0


cosx+(1/2)=0 или 2sinx-1=0


cosx+(1/2)=0

cosx=-1/2

x= ±(2π /3)+2πn, n ∈ [b]Z[/b]


или

2sinx-1=0

sinx=1/2

x=(-1)^(k)*(π/6)+πk, k ∈ [b]Z[/b]

О т в е т. a) ±(2π /3)+2πn, n ∈ [b]Z[/b]; (-1)^(k)*(π/6)+πk, k ∈ [b]Z[/b]

б)

1)
-(2π /3)+2πn, n ∈ [b]Z[/b] - корни этой серии не принадлежат указанному отрезку

2)
(2π /3)+2πn, n ∈ [b]Z[/b];

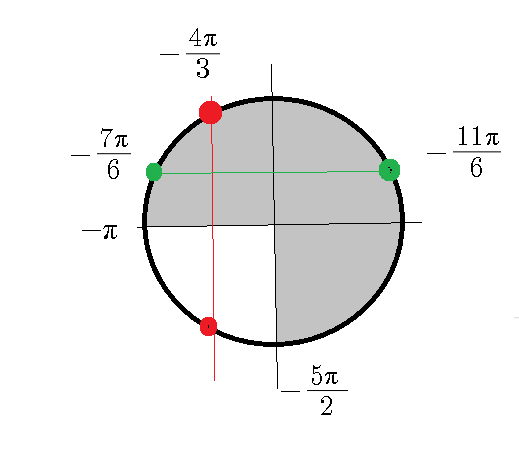
-5π/2 ≤ (2π /3)+2πn ≤ -π

Делим на π

-5/2 ≤ (2 /3)+2n ≤ -1

Умножаем на 6:

-15 ≤ 4+12n ≤ -6

Вычитаем 4:

-19 ≤ 12n ≤ -10

Неравенство верно для n= -1

Значит, корень уравнения, принадлежащий этому промежутку

x=(2π /3)+2π*(-1) ⇒ [b]х=-4π/3[/b]

3)
x=(-1)^(k)*(π/6)+πk, k ∈ [b]Z[/b]

при k=2m
x=(π/6)+2πm

Указанному промежутку принадлежит корень

х=(π/6)-2π ⇒ [b]х=-11π/6[/b]


при k=2m+1
x=(5π/6)+2πm

Указанному промежутку принадлежит корень

х=(5π/6)-2π ⇒ [b]х=-7π/6[/b]