Задача 77419 С помощью интегральной формулы Коши...
Условие
данный интеграл по контуру: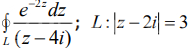
математика ВУЗ
226
Решение
★
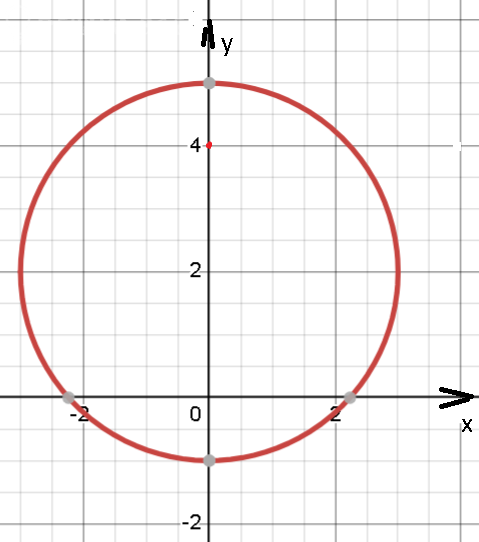
точка z=4i принадлежит области
По теореме Коши:
[m] ∫ _{|z-2i|=3}\frac{e^{-2z}}{z-4i}dz=2πi\cdot |e^{-2z}|_{z=4i}=2πi\cdot |e^{-2\cdot 4i}|=2πi\cdot |e^{-8i}|=2πi\cdot |cos(-8)+isin(-8)|=2πi\cdot \sqrt{(cos(-8))^2+(sin(-8))^2}=[/m]
[m]=2πi\cdot \sqrt{1}=2πi[/m]