Задача 77192 ...
Условие
математика колледж
173
Решение
★
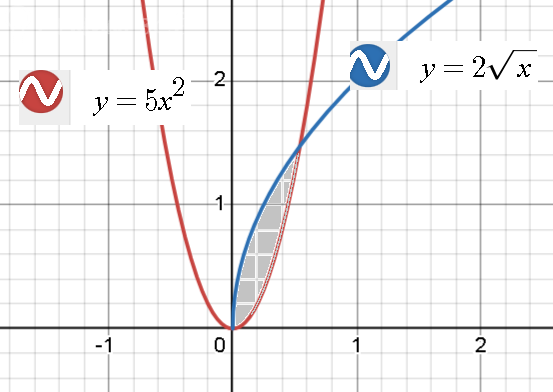
5x^2=2sqrt(x)
Возводим в квадрат
25x^4=4x
25x^4-4x=0
x*(25x^3-4)=0
x=0 или x=[m]\sqrt[3]{\frac{4}{25}}[/m]
[a;b]=[0;[m]\sqrt[3]{\frac{4}{25}}[/m]]
По правилу ( см. скрин)
[m]f(x)=2\sqrt{x}[/m]
[m]g(x)=5x^2[/m]
[m]S= ∫ ^{\sqrt[3]{\frac{4}{25}}}_{0}(2\sqrt{x}-5x^2)dx=(2\frac{x^{\frac{3}{2}}}{\frac{3}{2}}-5\frac{x^3}{3})|^{\sqrt[3]{\frac{4}{25}}}_{0}=\frac{4}{3}(\sqrt[3]{\frac{4}{25}})^{\frac{3}{2}}-\frac{5}{3}(\sqrt[3]{\frac{4}{25}})^3=\frac{4}{3}\cdot \frac{2}{5}-\frac{5}{3}\cdot \frac{4}{25}=\frac{8}{15}-\frac{4}{15}=\frac{4}{15}[/m]