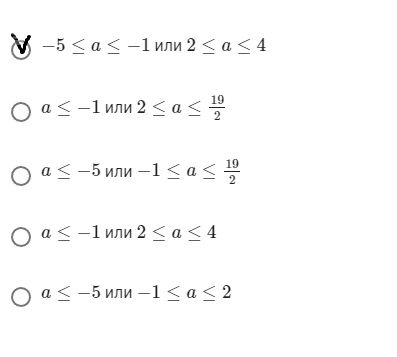Задача 77190 Найдите все значения параметра a, при...

Адель_486335203

30 апреля 2024 г. в 06:59

Найдите все значения параметра a, при каждом из которых уравнение

| – a² – a + x + 18| + | – a² + a + x – 1| = 2a – 19

имеет корни, но ни один из них не принадлежит интервалу (2; 3).

exponenta

30 апреля 2024 г. в 04:31

★

Найдем значения х, при которых подмодульные выражения меняют знак

–a²–a+x+18=0 ⇒ x=a²+a–18

–a²+x+x–1=0 ⇒ x=a²–a+1


Уравнение имеет корни, но они не принадлежат (2;3)

Значит
x ≤ 2 или x ≥ 3

Рассматриваем случаи:
1)
a²+a–18 ≤ 2 ⇒ a²+a–20 ≤ 0 ⇒ –5 ≤ a ≤ 4
a²–a+1 ≤ 2 ⇒

2)
a²+a–18 ≥ 3
a²–a+1 ≥ 3

3)
a²+a–18 ≤ 2⇒ a²+a–20 ≤ 0 ⇒ –5 ≤ a ≤ 4
a²–a+1 ≥ 3 ⇒ a²–a–2 ≥ 0 ⇒ a ≤–1 или a ≥ 2

–5 ≤ a ≤ –1 или 2 ≤ a ≤ 4

4)
a²+a–18 ≥ 3
a²–a+1 ≤ 2