Задача 75964 решите неравенство...
Условие
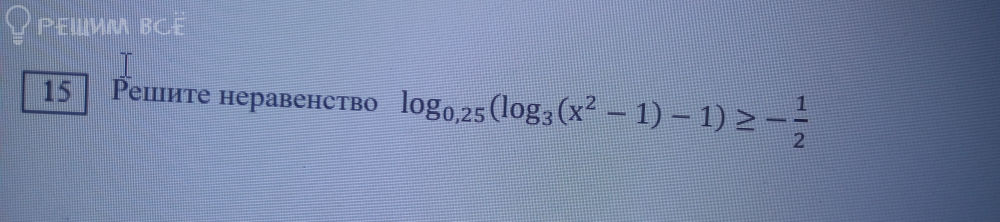
Решение
[m]0,25^{-\frac{1}{2}}=(\frac{1}{4})^{-\frac{1}{2}}=2
Логарифмическая функция с основанием [m]0,25[/m] [i] убывающая[/i], в третьем неравенстве меняем знак неравенства ( ≥ ) на ( ≤ )
[m]\left\{\begin {matrix}|x| >1\\log_{3}(x^2-1) >log_{3}3\\log_{3}(x^2-1)-1 ≤ 0,25^{-\frac{1}{2}}\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}|x| >1\\x^2-1 >3\\log_{3}(x^2-1) ≤ 2+1\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}|x| >1\\x^2 >4\\log_{3}(x^2-1) ≤log_{3}27\end {matrix}\right.[/m]
Логарифмическая функция с основанием [m]3[/m] [i] возрастающая[/i], в третьем неравенстве оставляем знак неравенства прежним
[m]\left\{\begin {matrix}|x| >1\\|x|>2\\x^2-1 ≤27\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}|x| >1\\|x|>2\\x^2 ≤28\end {matrix}\right.[/m]
28=4*7
sqrt(28)=2sqrt(7)
[m]\left\{\begin {matrix}|x| >1\\|x|>2\\|x| ≤2\sqrt{7}\end {matrix}\right.[/m]
О т в е т. [-2sqrt(7);-2) U (2;2sqrt(7)]