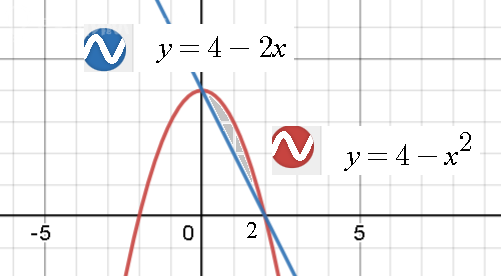
Задача 75847 Вычислить площадь фигуры, ограниченной...

65cdc5d46f194a26c45110af

2/15/2024 8:06:24 AM

Вычислить площадь фигуры, ограниченной графиками функций y=4–x^2,y=4-2x

5f3ea7e3faf909182968ddd9

2/15/2024 8:34:13 AM

★

Найдем абсциссы точек пересечения графиков:

4-x^2=4-2x

x^2-2x=0

x*(x-2)=0

[b]x=0[/b] или x-2=0 ⇒ [b]x=2[/b]

По правилу ( см. скрин 2)

[m]S= ∫ ^{2}_{0}( \underbrace{(4-x^2)}_{f_{2}(x)}-\underbrace{(4-2x)}_{f_{1}(x)})dx=∫ ^{2}_{0}(4-x^2-4+2x)dx=∫ ^{2}_{0}(2x-x^2)dx=[/m]


[m]=(x^2-\frac{x^3}{3})|^{2}_{0}=(2^2-\frac{2^3}{3})-(0^2-\frac{0^3}{3})=\frac{4}{3}[/m]