Задача 75617 ...
Условие
a) y = (x - 1)(x² - 5x + 4);
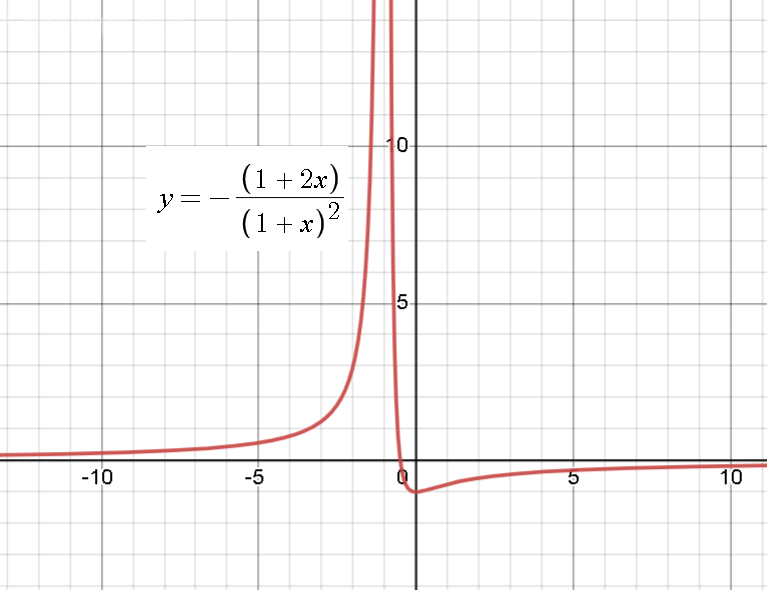
б) y = - (1 + 2x) / (1 + x)²;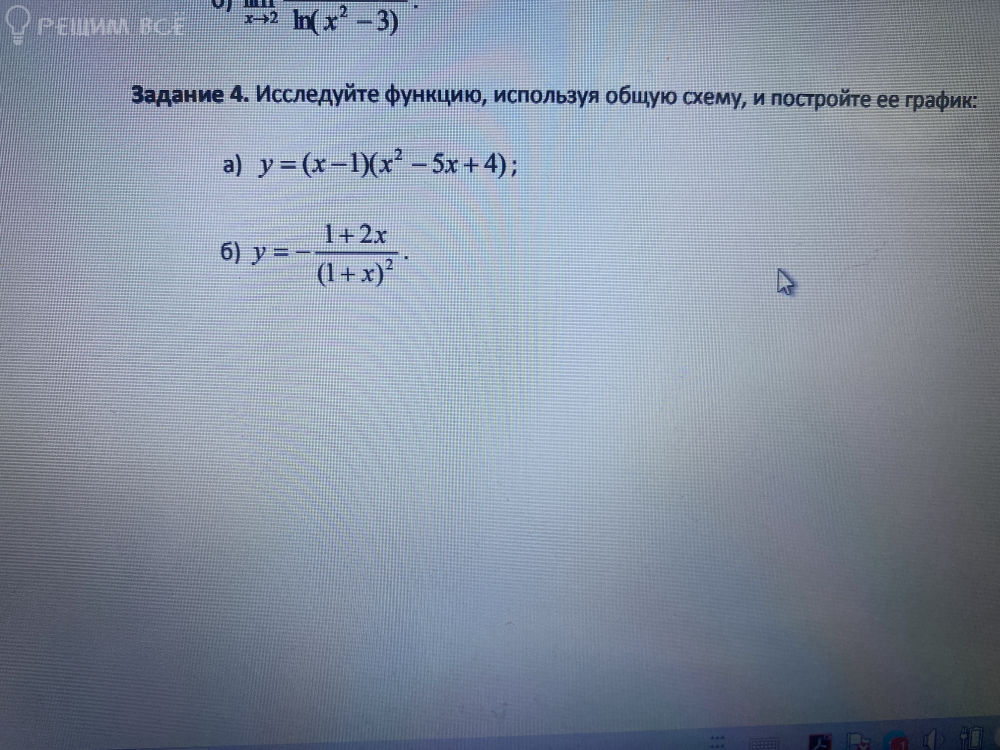
Решение
Область определения Не симметрична относительно 0 , значит
функция не является ни чётной, ни нечётной.
Функция не является периодической
Прямая [m] x=-1 [/m] является [i] вертикальной[/i] асимптотой.
Так как [m] lim_{x → -1}(-\frac{1+2 x}{(1+x)^2})=+ ∞ [/m]
[i]Горизонтальная[/i] асимптота [m]y=0[/m] , так как
[m] lim_{x → ∞}(-\frac{1+2 x}{(1+x)^2})= 0 [/m]
Наклонных асимптот нет, так как:
[m] k= lim_{x → ∞}\frac{f(x)}{x}=lim_{x → ∞}(-\frac{1+2 x}{(1+x)^2\cdot x})= 0[/m]
[b]Исследование с помощью первой производной[/b]:
[m]y`=(-\frac{1+2 x}{(1+x)^2})`[/m]
[m]y`=-\frac{(1+2 x)`\cdot (1+x)^2-(1+2x)\cdot ((1+x)^2)`}{((1+x)^2)^2}[/m]
[m]y`=-\frac{2\cdot (1+x)^2-(1+2x)\cdot 2(1+x)}{(1+x)^3}[/m]
[m]y`=-\frac{2+2x-2-4x}{(1+x)^3}[/m]
[m]y`=\frac{2x}{(1+x)^3}[/m]
y`=0
x=0
Расставляем знак производной на области определения
____+_ (-1) ___-___ (0) ____+__
y`>0 на (- ∞ ; -1) и на (0;+ ∞ )
Значит функция возрастает на (- ∞ ; -1) и на (0;+ ∞ )
y`<0 на (-1;0)
Значит, функция убывает на (-1;0)
x=0 - точка минимума, производная меняет знак с - на +
[m]y(-1)=\frac{1+2 \cdot (-1)}{(1-0)^2}=-1[/m]
[b]Исследование с помощью второй производной:[/b]
[m]y``=(y`)`=(\frac{(2x)}{(1+x)^3})`=\frac{2-4x}{(1+x)^4}[/m]
х=1/2 -[b] точка перегиба[/b]
[m]y`` >0 [/m] на (- ∞;-1) и на (-1;1/2) ⇒ функция выпукла вниз на (- ∞;-1) и на (-1;1/2)
[m]y`` <0 [/m] на(-1;1/2) ⇒ функция выпукла вверх на(-1;1/2)