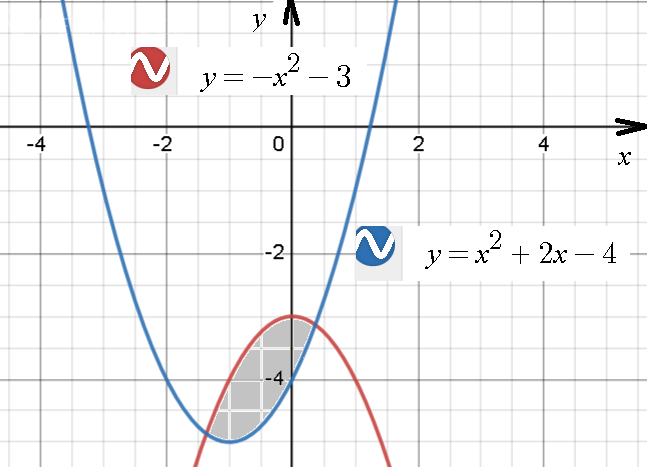
Задача 75525 найдите площадь фигуры, ограниченой...

65af45472cb5f04e9538b382

1/23/2024 4:50:10 AM

найдите площадь фигуры, ограниченой линиями у=х^2+2х-4 и у=-х^-3

5f3ea7e3faf909182968ddd9

1/23/2024 6:43:17 AM

★

x^2+2x-4=-x^2-3

2x^2+2x-1=0

D=2^2-4*2*(-1)=4+8=12

x_(1)=(-2-2sqrt(3))/4; x_(2)=(-2+2sqrt(3))/4;

x_(1)=(-1-sqrt(3))/2; x_(2)=(-1+sqrt(3))/2;



[m] S= ∫_{\frac{(-1-\sqrt{3}}{2}} ^{\frac{(-1+\sqrt{3}}{2}}(-x^2-3-(x^2+2x-4))dx= ∫_{\frac{(-1-\sqrt{3}}{2}} ^{\frac{(-1+\sqrt{3}}{2}}(1-2x-x^2)dx=[/m]

[m]=(x-x^2-\frac{x^3}{3})_{\frac{(-1-\sqrt{3}}{2}}| ^{\frac{(-1+\sqrt{3}}{2}}=(\frac{(-1+\sqrt{3}}{2}-(\frac{(-1+\sqrt{3}}{2})^2-\frac{(\frac{(-1+\sqrt{3}}{2})^3}{3})-(\frac{(-1-\sqrt{3}}{2}-(\frac{(-1-\sqrt{3}}{2})^2-\frac{(\frac{(-1-\sqrt{3}}{2})^3}{3})=...[/m]

считайте