Задача 75339 Доказать ограниченность числовой...
Условие
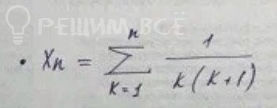
математика ВУЗ
282
Решение
★
[m]x_{2}=\frac{1}{1(1+1)}+\frac{1}{2(2+1)}=\frac{1}{2}+\frac{1}{6}=\frac{2}{3}[/m]
[m]x_{3}=\frac{1}{1(1+1)}+\frac{1}{2(2+1)}+\frac{1}{3(3+1)}=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}=\frac{3}{4}[/m]
...
[m]x_{n}=\frac{1}{1(1+1)}+\frac{1}{2(2+1)}+\frac{1}{3(3+1)}+...+\frac{1}{n(n+1)}[/m]
Последовательность [b]ограничена снизу[/b]
[m]\frac{1}{2}=x_{1} ≤ {x_{n}} [/m] ⇒
[m]inf( {x_{n}})=\frac{1}{2} [/m]