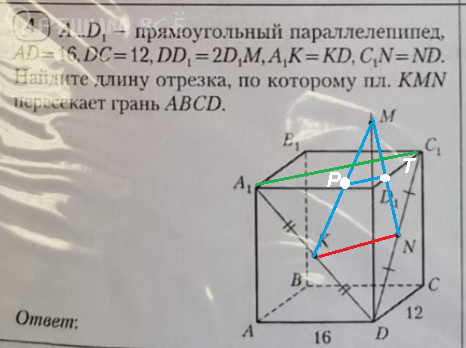
Задача 74752 Нужно решить все задания ????...
Условие
Решение
CD; C_(1)D_(1); CC_(1); DD_(1)
2)
BB_(1)C
В треугольнике АВ_(1)С
MK - средняя линия
МК || B_(1)C ⇒ МК || пл BB_(1)C
3)
AD=8
MK=4
Длина отрезка, соединяющего середины АМ и DK -
это длина средней линии трапеции АМKD
(8+4)/2=6
4)
АС^2=AB^2+BC^2=16^2+12^2=256+144=400
AC=20
А_(1)С_(1)=АС=20
КN=(1/2)А_(1)С_(1) = 10 - средняя линия Δ A_(1)BC_(1)
PT=(1/2)KN=5 - средняя линия Δ MKN
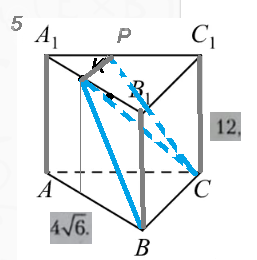
5)
S_(сеч)=S_(трапеции BKPC)=(1/2)(KP+BC)*h_( трапеции BKPC)
KP=(1/3)BC=(4sqrt(6)/3)
KB^2=12^2+(2*(4sqrt(6)/3))^2=144+(64/3)=496/3
h^2_( трапеции BKPC)=KB^2-((BC-KP)/2)^2=(496/3)-(4sqrt(6)/3)^2=(496-96)/3=400/3
h_( трапеции BKPC)=20./sqrt(3)
S_(сеч)=(1/2)((4sqrt(6)/3)+4sqrt(6))*20/sqrt(3)=80sqrt(2)