Задача 74625 Найдите радиус шара, вписанного в...

643af077b5eff0214304b241

12/9/2023 6:27:07 AM

Найдите радиус шара, вписанного в правильную шестиугольную пирамиду, если ее апофема равна L, а двугранный угол пирамиды при ребре основания равен а.

5f3ea7e3faf909182968ddd9

12/9/2023 8:37:15 AM

★

Апофема равна L ⇒[b] SP=L[/b]
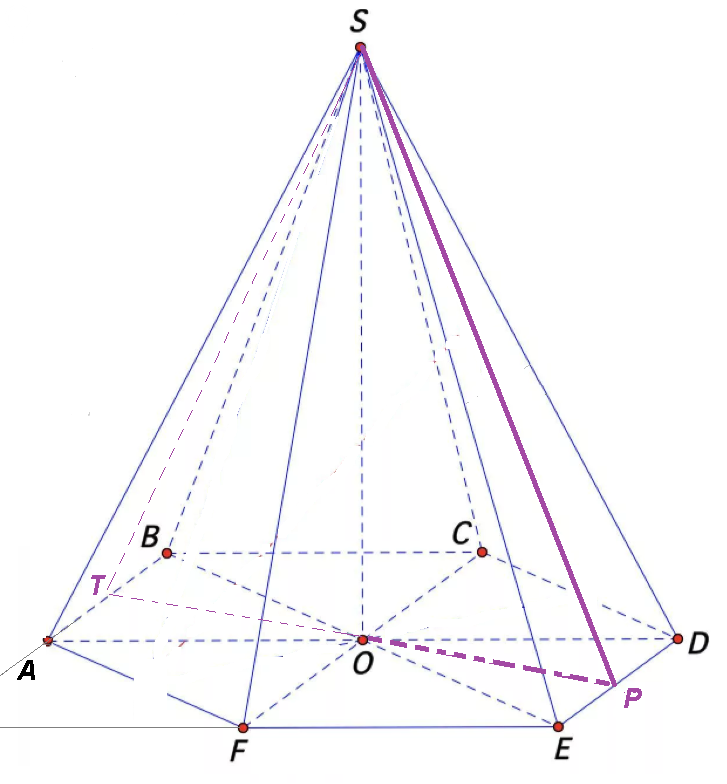
Двугранный угол пирамиды при ребре основания равен α ⇒ ∠ SPO= α

SO=L*sin α
OP=L*cos α
OP- высота [i]равностороннего[/i] треугольника DOE
Найти радиус шара, значит найти радиус окружности, вписанной в [i] равнобедренный[/i] треугольник
STP

ST=SP=[b]L[/b]
TP=2*OP=2*L*cos α

Применяем формулу:
R=abc/4S

S_( Δ STP)=(1/2)*TP*SO=(1/2)*(2*L*cos α)*(L*sin α) =L^2*sin α *cos α


R=(L*L*2*L*cos α)/(4*L^2*sin α *cos α )=L/(2sin α )