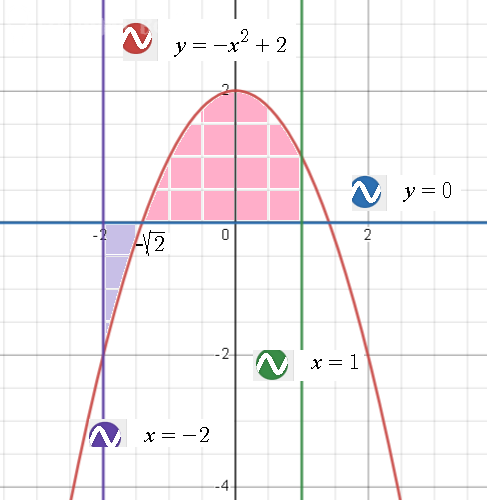
Задача 74479 Вычислите площадь фигуры ограниченной...

656ad8300d797a6d556c564d

12/2/2023 7:41:02 AM

Вычислите площадь фигуры ограниченной линиями: y=-x^2+2; y=0; x=1; x=-2. Ответ с графиком

5f3ea7e3faf909182968ddd9

12/2/2023 9:08:26 AM

★

[m]-x^2+2=0[/m] ⇒ [m]x= ± \sqrt{2}[/m]



[m]S=S_{1}+S_{2}[/m]

[m]S_{1}= ∫^{ - \sqrt{2}}_{-2} (0-(-x^2+2))dx=∫^{- \sqrt{2}}_{-2}(x^2-2)dx=(\frac{x^3}{3}-2x)|^{- \sqrt{2}}_{-2}=(\frac{(- \sqrt{2})^3}{3}-2\cdot( - \sqrt{2}))-(\frac{(-2)^3}{3}-2\cdot (-2))=-\frac{2\sqrt{2}}{3}+2\sqrt{2}+\frac{8}{3}-4=[/m]

[m]=\frac{4\sqrt{2}}{3}-\frac{4}{3}[/m]

[m]S_{2}= ∫^{1}_{- \sqrt{2}} (-x^2+2-0)dx=(-\frac{x^3}{3}+2x)|^{1}_{- \sqrt{2}} =(-\frac{1^3}{3}+2\cdot 1)-(-\frac{(- \sqrt{2})^3}{3}+2\cdot (- \sqrt{2}))=\frac{5}{3}-\frac{2\sqrt{2}}{3}+2\sqrt{2}=\frac{5}{3}+\frac{4\sqrt{2}}{3}[/m]


[m]S=\frac{4\sqrt{2}}{3}-\frac{4}{3}+\frac{5}{3}+\frac{4\sqrt{2}}{3}=\frac{1+8\sqrt{2}}{3}[/m]