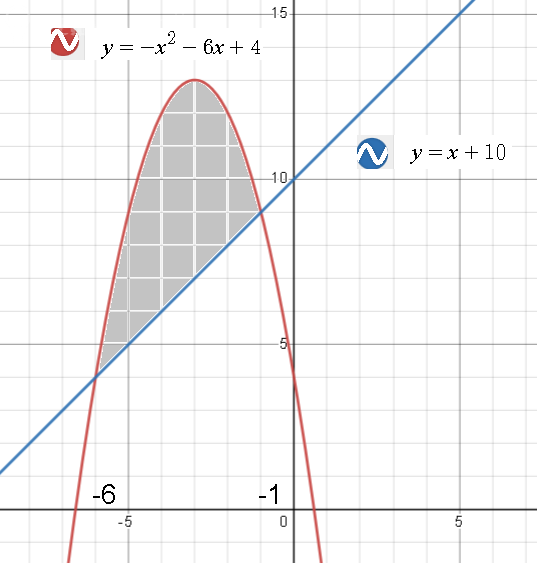
Задача 74478 Вычислите площадь фигуры ограниченной...
Условие
математика колледж
217
Решение
★
-x^2-7x-6=0
x^2+7x+6=0
x_(1)=[b]-6[/b]; x_(2)=[b]-1[/b]
[m]S= ∫^{ -1}_{-6} ((-x^2-6x+4)-(x+10))dx=∫^{ -1}_{-6}(-x^2-7x-6)dx=(-\frac{x^3}{3}-7\frac{x^2}{2}-6x)|^{-1}_{-6}=[/m]
[m]=(-\frac{(-1)^3}{3}-7\frac{(-1)^2}{2}-6\cdot (-1))-(-\frac{(-6)^3}{3}-7\frac{(-6)^2}{2}-6\cdot (-6))=\frac{1}{3}-\frac{7}{2}+6-\frac{216}{3}+\frac{252}{2}-36=[/m]
[m]=\frac{125}{6}[/m]