Задача 74292 Номер 2 нужен с проверкой Номер 3 нужны...
Условие
Номер 3 нужны графики 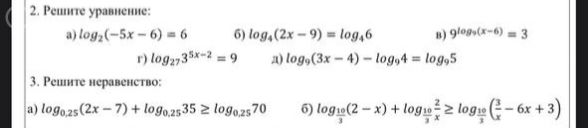
Решение
a) log_(2)(-5x-6)=6
По определению логарифма
(-5х-6)=2^6
-5x-6=64
-5x=64+6
-5x=70
x=-70/5
x=-14
Проверка
log_(2)(-5*(-14)-6)=6
log_(2)(70-6)=6
log_(2)64=6
6=6 - верно
О т в е т. 6
б)
log(4)(2x–9)=log_(4)6
По свойству монотонности логарифмической функции. Если логарифмы равны, то и аргументы равны
2х-9=6
2х=6+9
2х=15
х=7,5
Проверка
log(4)(2*7,5–9)=log_(4)6
log_(2)(15-9)=log_(4)6
log_(4)6=log_(4)6 - верно
О т в е т. 7,5
в)
[m]9^{log_{9}(x-6)}=3[/m]
Применяем основное логарифмическое тождество: [m]a^{log_{a}b}=b[/m], [m] a>0; b>0; a ≠ 1[/m]
[m]x-6=3[/m]
[m]x=3+6[/m]
[m]x=9[/m]
Проверка
[m]9^{log_{9}(9-6)}=3[/m]
[m]9^{log_{9}3}=3[/m]
3=3- верно
О т в е т. 9
3.
[m]log_{0,25}(2x-7)+log_{0,25}35 ≥log_{0,25}70 [/m]
Неравенство имеет смысл при [m]2x-7>0[/m] ⇒ [red] [m]x>3,5[/m]
[/red]
Применяем свойства логарифмов:
[m]log_{0,25}(2x-7)\cdot 35 ≥log_{0,25}70 [/m]
Логарифмическая функция с основанием [m]0<0,25 < 1[/m] [i] монотонно убывающая[/i]
БОльшему значению функции соответствует меньшее значение аргумента:
[m](2x-7)\cdot 35 ≤ 70 [/m]
[m](2x-7) ≤ 2 [/m]
[m]2x ≤ 2+7 [/m]
[m]x ≤ 4,5 [/m]
C учетом условия [red] [m]x>3,5[/m]
[/red]получаем ответ:
[m]3,5 < x ≤ 4,5 [/m]
О т в е т. (3,5; 4,5]