Задача 73963 ...
Условие
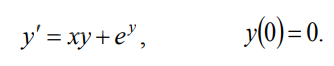
математика ВУЗ
274
Решение
★
y`(0)=[b]1[/b]
y``=(xy+e^(y))`=(x)`*y+x*y`+e^(y)*y`=y+x*y`+e^(y)*y`
y``(0)=y(0)+0*y`(0)+e^(0)*y`(0)=0+0+1*1=1
y``(0)=1
y```=(y+x*y`+e^(y)*y`)`=y`+x`*y+x*y`+e^(y)*y`*y`+e^(y)*y``
y```(0)=1+0+1+1=3
y````=(y`+y+x*y`+e^(y)*y`*y`+e^(y)*y``)`=
и так далее
По формуле Тейлора
y=y(0)+y`(0)*x+(y``(0)/2!)*x^2+(y```(0)/3!)*x^3+(y```(0)/4!)*x^4+...
y=0+[b]1[/b]*x+(1/2!)x^2+(3/3!)x^3+...
