Задача 73426 а) Решите уравнение tgx-sinx+cosx=1 б)...
Условие
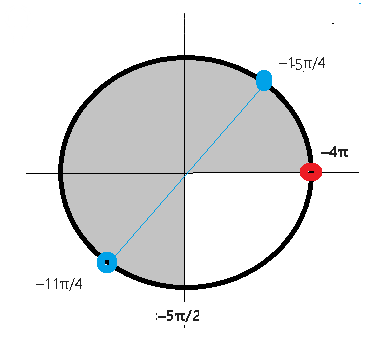
б) Найдите все корни этого уравнения, принадлежащие отрезку [-4Pi; -5Pi/2] .
Решение
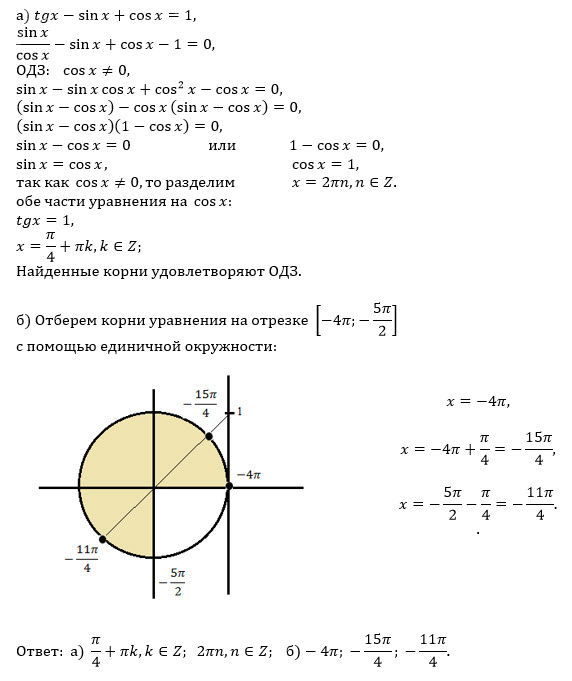
Все решения
[m](\frac{sinx}{cosx}-sinx)+(cosx-1)=0[/m]
[m]sinx(\frac{1}{cosx}-1)+(cosx-1))=0[/m]
[m]sinx\cdot\frac{1-cosx}{cosx}-(1-cosx)=0[/m]
[m](1-cosx)(\frac{sinx}{cosx}-1)=0[/m]
[m](1-cosx)\frac{sinx-cosx}{cosx}=0[/m]
[m]\left\{\begin {matrix}1-cosx=0\\cosx ≠ 0\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}sinx-cosx=0\\cosx ≠ 0\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}cosx=1\\cosx ≠ 0\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}tgx=1\\cosx ≠ 0\end {matrix}\right.[/m]
[m]\left\{\begin {matrix}x=2πn, n ∈ Z\\cosx ≠ 0\end {matrix}\right.[/m] или [m]\left\{\begin {matrix}x=\frac{π}{4}+πk, k ∈ Z\\cosx ≠ 0\end {matrix}\right.[/m]
О т в е т
a) [m]2πn, n ∈ Z;\frac{π}{4}+πk, k ∈ Z[/m]
О т в е т.
б)[b]-4π ∈ [-4π;-5π/2][/b]
Отбираем корни с помощью неравенства:
-4π ≤ 2πn ≤ -5π/2, n ∈ Z
Делим на π:
⇒ -4 ≤ 2n ≤ -5/2 ⇒ неравенство верно при n=-2
Находим корень
при n=-2
2π*(-2)=-4π
[b]-4π ;-15π/4 ;- 11π/4 ∈ [-4π;-5π/2][/b]
-4π ≤ [m]\frac{π}{4}[/m]+πk ≤ -5π/2, k ∈ Z ⇒-4 ≤ [m]\frac{1}{4}[/m]+k ≤ -5/2, k ∈ Z
Неравенство верно
при k=-3; k=-4
Находим эти корни
-4π ≤ [m]\frac{π}{4}[/m]+π* (-3) ≤ -5π/2, k ∈ Z
-4π ≤ [m]\frac{π}{4}[/m]+π* (-4) ≤ -5π/2, k ∈ Z
[b]-15π/4 ;- 11π/4 ∈ [-4π;-5π/2][/b]
Отбор корней помощью единичной окружности см на рис.