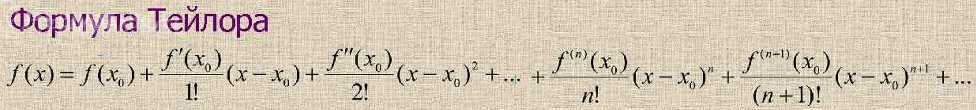Задача 72058 Найти решение дифференциального...

648a0cc453b882663c41869e

14.06.2023 22:08:20

Найти решение дифференциального уравнение в виде степенного ряда (четыре ненулевых члена).
y" – 2xy'– у=x5, если y(1)=1,y'(1)=2.

5f3ea7e3faf909182968ddd9

15.06.2023 09:43:07

★

Подставляем в данное уравнение:
x=1
y(1)=1
y`(1)=2

y``(1)-2*1y`(1)-y(1)=1^5 ⇒ y``(1)=2*2+1+1
y``(1)=6


Дифференцируем равенство

y" – 2xy'– у=x^5

y```-2y`-2xy``-y`=5x^4

Подставляем в это уравнение:
x=1
y(1)=1
y`(1)=2
y``(1)=6


y```(1)=2*2+2*1*6+2+5*1^4
y```(1)=23

Подставляем в формулу Тейлора

[m]y=1+\frac{2}{1!}(x-1)+\frac{6}{2!}(x-1)^2+\frac{23}{3!}(x-1)^3[/m]