Задача 72039 Исследовать на сходимость данные...
Условие
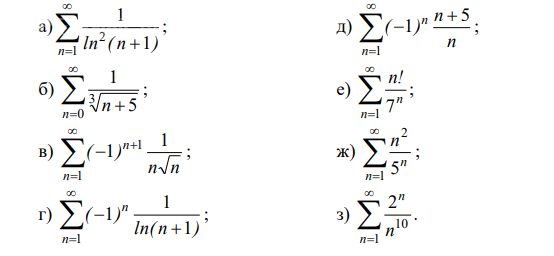
Решение
[m]∑^{ ∞} _{n=1} \frac{1}{n^{p}}[/m] - обобщенный гармонический ряд.
Сходится при p >1
Расходится при p ≤ 1
[m]∑^{ ∞} _{n=1} \frac{1}{\sqrt[3]{n+5}}[/m] эквивалентен ряду [m]∑^{ ∞} _{n=1} \frac{1}{\sqrt[3]{n}}[/m], который расходится
p=1/3 < 1
Данный ряд расходится по признаку сравнения с [m]∑^{ ∞} _{n=1} \frac{1}{\sqrt[3]{n}}[/m]
в)
Ряд из модулей [m]∑^{ ∞} _{n=1} \frac{1}{n\sqrt{n}}[/m] сходится, как обобщенный гармонический ряд при p=3/2
Данный ряд сходится абсолютно
г)
Знакочередующийся ряд сходится по признаку Лейбница
1) |a_(n)|=1/ln(n+1) → 0 при n → ∞
2)(a_(n))^( ∞) _(n=1) монотонно убывающая последовательность
f(x)=1/ln(x+1) - монотонно убывающая функция
f`(x)=-1/ln^2(x+1)< 0 при x >0
Ряд из модулей
[m]∑^{ ∞} _{n=1} \frac{1}{ln(n+1)}[/m] расходится, так как
[m]\frac{1}{n+1} < \frac{1}{ln(n+1)}[/m]
Ряд [m] ∑^{ ∞} _{n=1} \frac{1}{n+1}[/m] расходится как эквивалентный ряду [m]∑^{ ∞} _{n=1} \frac{1}{n}[/m]
Данный ряд сходится условно
д) Ряд расходится. Не выполняется необходимое условие сходимости
Общий член ряда не стремится к 0
e)
Ряд расходится по признаку Даламбера
[m]lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{(n+1)!}{7^{n+1}}}{\frac{n!}{7^{n}}}=\frac{1}{7}lim_{n → ∞ }(n+1) >1[/m]
ж)
Ряд сходится по признаку Даламбера
[m]lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{(n+1)^2}{5^{n+1}}}{\frac{n^2}{5^{n}}}=\frac{1}{5}lim_{n → ∞ }\frac{(n+1)^2}{n^2}=\frac{1}{5}\cdot 1=\frac{1}{5} <1[/m]
з)
Ряд расходится по признаку Даламбера
[m]lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}=2 >1[/m]

