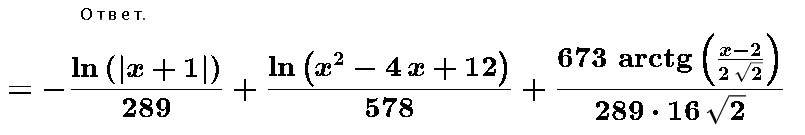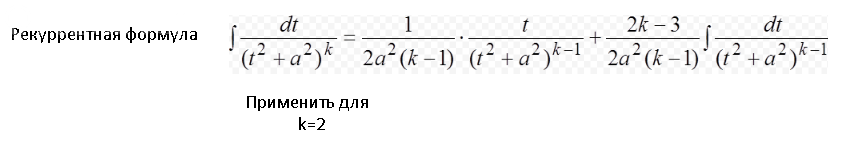Задача 71855 ...
Условие
Решение
D=(-4)^2-4*12<0
Раскладываем подынтегральную дробь на простейшие
[m]\frac{-x^2+6x+6}{(x+1)(x^2-4x+12)^2}=\frac{A}{x+1}+\frac{Mx+N}{x^2-4x+12}+\frac{Tx+P}{(x^2-4x+12)^2}[/m]
[m]\frac{-x^2+6x+6}{(x+1)(x^2-4x+12)^2}=\frac{A(x^2-4x+12)^2+(Mx+N)(x+1)(x^2-4x+12)+(Tx+P)(x+1)}{(x^2-4x+12)^2}[/m]
Приравниваем числители
[m]-x^2+6x+6=Ax^4+16Ax^2+144A-8Ax^3+24Ax^2-96Ax+Mx^4+Nx^3+Mx^3+Nx^2-4Mx^3-4Nx^2-4Mx^2-4Nx+[/m]
[m]+12Mx^2+12Nx+12Mx+12N+Tx^2+Px+Tx+P[/m]
Приравниваем коэффициенты при одинаковых степенях переменной
x^4:
0=A+M
x^3:
0=N+M-4M-8A
x^2:
-1=16A+24A+N-4N-4M+12M+T
x:
6=-96A-4N+12N+12M+P+T
x^0:
6=144A+12N+P
[m]\left\{\begin {matrix}A+M=0 ⇒ M=-A\\N-3M-8A=0 ⇒N=5A\\40A-3N+8M+T=-1 ⇒T=-1-17A\\-96A+8N+12M+P+T=6 ⇒ P=85A+7\\144A+12N+P=0 ⇒ 144A+60A+85A+7=6 \end {matrix}\right.[/m]
Решаем систему и находим
A=-[m]\frac{1}{289}[/m]
M=[m]\frac{1}{289}[/m]
N=-[m]\frac{5}{289}[/m]
T=-[m]\frac{272}{289}[/m]
P=[m]\frac{1938}{289}[/m]
[m] ∫ \frac{-x^2+6x+6}{(x+1)(x^2-4x+12)^2}dx= ∫ \frac{A}{x+1}dx+ ∫ \frac{Mx+N}{x^2-4x+12}dx+ ∫ \frac{Tx+P}{(x^2-4x+12)^2}dx[/m]
1)
[m]∫ \frac{A}{x+1}dx=-\frac{1}{289}∫ \frac{1}{x+1}dx==-\frac{1}{289}ln|x+1|[/m]
2)
[m]∫ \frac{Mx+N}{x^2-4x+12}dx=\frac{1}{289}∫ \frac{x-5}{x^2-4x+12}dx[/m]
Выделяем полный квадрат
[m]x^2-4x+12=x^2-4x+4+8=(x-2)^2+8[/m]
[m]=\frac{1}{289}∫ \frac{x-5}{(x-2)^2+8}dx=[/m]
[i]замена переменной[/i]
[m]x-2=t[/m]
[m]x=t+2[/m]
[m]dx=dt[/m]
[m]=\frac{1}{289}∫ \frac{t+2-5}{t^2+8}dt=\frac{1}{289} ∫ \frac{t}{t^2+8} dt-\frac{3}{289} ∫\frac{1}{t^2+8}dt=[/m]
[m]=\frac{1}{578}ln(t^2+8)-\frac{3}{289\cdot 2\sqrt{2}}arctg\frac{t}{2\sqrt{2}}=\frac{1}{578}ln(x^2-4x+12)-\frac{3}{289\cdot 2\sqrt{2}}arctg\frac{x-2}{2\sqrt{2}}[/m]
Первый интеграл табличный [m] ∫ \frac{du}{u}=ln|u|[/m]
Второй интеграл табличный [m]∫\frac{1}{t^2+8}dt=\frac{1}{2\sqrt{2}}arctg\frac{t}{2\sqrt{2}}[/m]
3)
[m] ∫ \frac{Tx+P}{(x^2-4x+12)^2}=[/m]
Выделяем полный квадрат
[m]x^2-4x+12=x^2-4x+4+8=(x-2)^2+8[/m]
[i]замена переменной[/i]
[m]x-2=t[/m]
[m]x=t+2[/m]
[m]dx=dt[/m]
[m] ∫ \frac{Tx+P}{(x^2-4x+12)^2}dx= \frac{1}{289} ∫ \frac{(-272(t+2)+1938)}{(t^2+8)^2} dt =-\frac{136}{289} ∫ \frac{2t}{(t^2+8)^2} dt+\frac{1394}{289}∫ \frac{1}{(t^2+8)^2}dt [/m]
Первый интеграл табличный [m] ∫ \frac{du}{u^2}=-\frac{1}{u}[/m]
Второй интеграл (применяем рекуррентную формулу)
[m]∫ \frac{1}{(t^2+8)^2}dt=\frac{t}{16(t^2+8)}+\frac{1}{16} ∫ \frac{dt}{t^2+8}=\frac{t}{16(t^2+8)}+\frac{1}{16\cdot 2\sqrt{2}}arctg\frac{t}{2\sqrt{2}}=\frac{x-2}{16(x^2+4x-12)}+\frac{1}{16\cdot 2\sqrt{2}}arctg\frac{x-2}{2\sqrt{2}} [/m]
Итак,
[m] ∫ \frac{-x^2+6x+6}{(x+1)(x^2-4x+12)^2}dx= -\frac{1}{289}∫ \frac{1}{x+1}dx+\frac{1}{289}∫ \frac{x-5}{x^2-4x+12}dx+\frac{1}{289} ∫\frac{(-272x+1938)}{(x^2-4x+12)^2}dx = [/m]
[m]=-\frac{1}{289}ln|x+1|+\frac{1}{578}ln(x^2-4x+12)-\frac{3}{289\cdot 2\sqrt{2}}arctg\frac{x-2}{2\sqrt{2}}+\frac{136}{289}\frac{1}{x^2-4x+12}+\frac{1394(x-2)}{16\cdot 289(x^2-4x+12)}+\frac{1394}{16\cdot 289\cdot 2\sqrt{2}}arctg\frac{x-2}{2\sqrt{2}}= [/m]
[m]=-\frac{1}{289}ln|x+1|+\frac{1}{578}ln(x^2-4x+12)+\frac{1346}{289\cdot 2\sqrt{2}}arctg\frac{x-2}{2\sqrt{2}}+\frac{136}{289}\frac{1}{x^2-4x+12}+\frac{1394(x-2)}{16\cdot 289(x^2-4x+12)}= [/m]