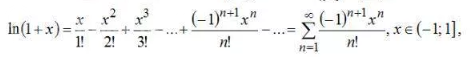Задача 71822 В разложении функции в ряд Тейлора -...

6320a99c26d9cc47f00fe39a

26.05.2023 22:29:58

В разложении функции в ряд Тейлора - Маклорена. Найти a6

5f3ea7e3faf909182968ddd9

26.05.2023 22:43:01

★

[m]ln(1+x)=\frac{x}{1!}-\frac{x^2}{2!}+\frac{x^3}{3!}-\frac{x^4}{4!}+\frac{x^5}{5!}+\frac{x^6}{6!}+...[/m]

[m]6\cdot ln(1+x)=6\cdot \frac{x}{1!}-6\cdot \frac{x^2}{2!}+6\cdot \frac{x^3}{3!}-6\cdot \frac{x^4}{4!}+6\cdot \frac{x^5}{5!}+6\cdot \frac{x^6}{6!}+...[/m]


[m]a_{6}x^{6}=6\cdot \frac{x^6}{6!}[/m] ⇒ [m]a_{6}=6\frac{1}{6!}[/m] ⇒ [m]a_{6}=\frac{1}{120}[/m]