Задача 71659 y'+2xy=y^2e^x^2 Решить дифф уравнение...
Условие
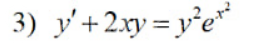
Решение
[m]y`+p(x)y=f(x)\cdot y^{n}[/m], n ≠ 1
[m]p(x)=2x[/m]
[m]f(x)=e^{x^2}[/m]
Делим обе части уравнения на [m]y^2[/m]
[m]\frac{y`}{y^2}+\frac{2x}{y}=e^{x^2}[/m]
Замена переменной:
[m] z=\frac{1}{y}[/m] ⇒ [m] y=\frac{1}{z}[/m]
[m] y`=-\frac{1}{z^2}\cdot z`[/m] ⇒ [m] y`=-y^2\cdot z`[/m]
Уравнение принимает вид:
[m]\frac{(-y^2\cdot z`)}{y^2}+2xz=e^{x^2}[/m] ⇒ [m]-z`+2xz=e^{x^2}[/m]- линейное уравнение первого порядка.
Решаем методом Бернулли: находим решение в виде произведения двух функций
[m]z=u\cdot v[/m]
[m]z`=u`\cdot v+u\cdot v`[/m]
Подставляем в уравнение:
[m]-z`+2xz=e^{x^2}[/m]
[m]-u`\cdot v-u\cdot v`+2xu\cdot v=e^{x^2}[/m]
Группируем:
[m]-u`\cdot v-u\cdot (v`-2x \cdot v)=e^{x^2}[/m]
Полагаем
[m](v`-2x \cdot v)=0[/m]
Тогда
[m]-u`\cdot v-u\cdot 0=e^{x^2}[/m]
Решаем два уравнения с [i]разделяющимися[/i] переменными:
[m](v`-2x \cdot v)=0[/m] ⇒ [m]\frac{dv}{v}=2xdx[/m] ⇒ [m] ∫ \frac{dv}{v}= ∫ 2xdx[/m] ⇒[m] lnv=x^2 ⇒ v=e^{x^2}[/m]
⇒
[m]-u`\cdot e^{x^2}-u\cdot 0=e^{x^2}[/m] ⇒ [m]-u`=1[/m] ⇒ [m]du=-dx[/m] ⇒ [m] ∫ du=- ∫ dx[/m] ⇒ [m]u=-x+C[/m]
[m]z=(-x+C)\cdot e^{x^2}[/m]
Обратный переход к переменной y:
[m]y=\frac{1}{(-x+C)\cdot e^{x^2}}[/m]
