Задача 71340 Решить дифференциальное уравнение. Найти...
Условие
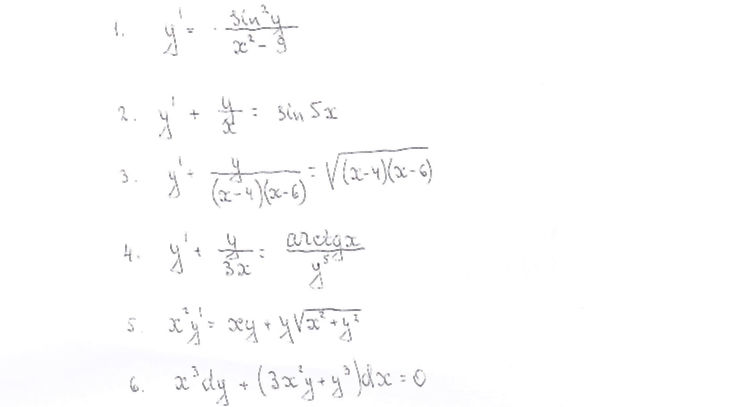
Решение
[m]y`+\frac{y}{x}=sin5x[/m]- линейное дифференциальное уравнение 1-го порядка вида
[m]y`+p(x)y=f(x)[/m],
[m]p(x)=\frac{1}{x}[/m]
[m]f(x)=sin5x[/m]
Находим решение в виде произведения двух функций
[m]y=u\cdot v[/m]
[m]y`=u`\cdot v+u\cdot v`[/m]
подставляем в уравнение
[m]u`\cdot v+u\cdot v`+\frac{1}{x}u\cdot v=sin5x[/m]
Группируем
[m]u`\cdot v+u\cdot (v`+\frac{1}{x}\cdot v)=sin5x[/m]
Полагаем
[m](v`+\frac{1}{x}\cdot v)=0[/m]
Тогда
[m]u`\cdot v+u\cdot 0=sin5x[/m]
Решаем два уравнения с разделяющимися переменными
[m](v`+\frac{1}{x}\cdot v)=0[/m] ⇒ [m]\frac{dv}{v}=-\frac{dx}{x}[/m]
Интегрируем
[m] ∫ \frac{dv}{v}=- ∫ \frac{dx}{x}[/m]
[m]ln|v|=-ln|x|[/m] ⇒ ln|x|=ln|\frac{1}{x}|[/m] ⇒ [m]v=\frac{1}{x}[/m]
подставляем во второе
[m]u`\cdot \frac{1}{x}+u\cdot 0=sin5x[/m] ⇒ [m]du=x\cdot sin5xdx[/m]
Интегрируем
[m]u=x\cdot (-\frac{1}{5}cos5x)+\frac{1}{5} ∫ cos5xdx[/m] ( cм интегрирование по частям)
[m]u=x\cdot (-\frac{1}{5}cos5x)+\frac{1}{25}sin5x+C[/m]
[m]y=(-\frac{x}{5}cos5x)+\frac{1}{25}sin5x+C)\cdot \frac{1}{x}[/m]- общее решение
3)
[m]y`-\frac{1}{(x-4)(x-6)}\cdot y=\sqrt{(x-4)(x-6)}[/m]- линейное уравнение вида [m]y`+p(x) y=f(x)[/m]
[m]p(x)=\frac{1}{(x-4)(x-6)}[/m]
[m]f(x)=\sqrt{(x-4)(x-6)}[/m]
y=u*v
y`=u`*v+u*v`
Подставляем в уравнение:
[m]u`\cdot v+u\cdot v`-\frac{1}{(x-4)(x-6)}\cdot u\cdot v=\sqrt{(x-4)(x-6)}[/m]
Группируем
[m]u`\cdot v+u\cdot (v`-\frac{1}{(x-4)(x-6)}\cdot v)=\sqrt{(x-4)(x-6)}[/m]
1)
Полагаем
[m]v`+\frac{v}{(x-4)(x-6)}=0[/m] - уравнение с разделяющимися переменными
тогда
2)
[m]u`\cdot v=\sqrt{(x-4)(x-6)}[/m] - уравнение с разделяющимися переменными
Решаем первое:
[m]\frac{dv}{v}=\frac{1}{(x-4)(x-6)}dx[/m] - справа интеграл от дроби, раскладываем её на простейшие.
⇒
[m] ∫ \frac{dv}{v}= ∫ \frac{1}{(x-4)(x-6)}dx[/m]
[m]ln|v|= ∫( \frac{\frac{1}{2}}{x-6}- \frac{\frac{1}{2}}{x-4})dx[/m]
[m]ln|v|=\frac{1}{2}ln|x-6|-\frac{1}{2}ln|{x-4}[/m]
[m]ln|v|=ln\sqrt{\frac{x-6}{x-4}}[/m]
[m]v=\sqrt{\frac{x-6}{x-4}}[/m]
и подставляем во второе
[m]u`\cdot\sqrt{\frac{x-6}{x-4}}=\sqrt{(x-4)(x-6)}[/m]
[m]u`=(x-4)[/m]
[m]u= ∫ (x-4)dx[/m]
[m]u=\frac{x^2}{2}-4x+C[/m]
[m]u=\frac{x^2}{2}-4x+C[/m]
y=u*v
[m]y=(\frac{x^2}{2}-4x+C)\cdot \sqrt{\frac{x-6}{x-4}}[/m]- общее решение
