Задача 71227 Найдите линейные дифференциальные...
Условие
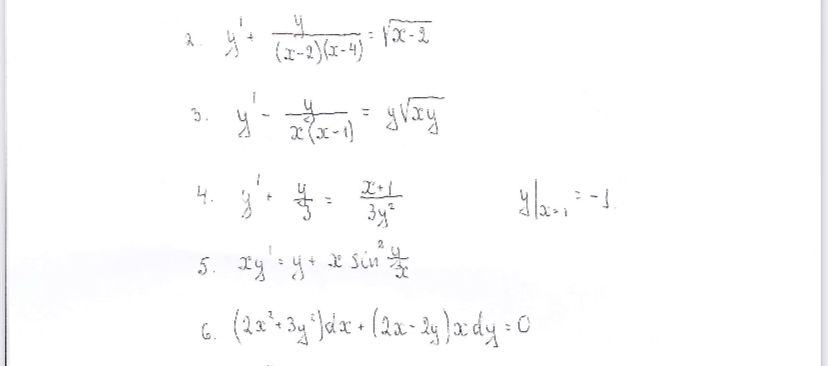
Решение
[m]y`+\frac{1}{(x-2)(x-4)}\cdot y=\sqrt{x-2}[/m]- линейное уравнение вида [m]y`+p(x) y=f(x)[/m]
y=u*v
y`=u`*v+u*v`
Подставляем в уравнение:
[m]u`\cdot v+u\cdot v`+\frac{1}{(x-2)(x-4)}\cdot u\cdot v=\sqrt{x-2}[/m]- линейное уравнение вида [m]y`+p(x) y=f(x)[/m]
Группируем
[m]u`\cdot v+u\cdot (v`+\frac{1}{(x-2)(x-4)}\cdot v)=\sqrt{x-2}[/m]
1)
Полагаем
[m]v`+\frac{v}{(x-2)(x-4)}=0[/m] - уравнение с разделяющимися переменными
тогда
2)
[m]u`\cdot v=\sqrt{x-2}[/m] - уравнение с разделяющимися переменными
Решаем первое:
[m]\frac{dv}{v}=-\frac{1}{(x-2)(x-4)}dx[/m]
⇒
[m] ∫ \frac{dv}{v}=- ∫ \frac{1}{(x-2)(x-4)}dx[/m]
[m]ln|v|=- ∫( \frac{\frac{1}{2}}{x-4}- \frac{\frac{1}{2}}{x-2})[/m]
[m]ln|v|=- \frac{1}{2}ln|(x-4)|+\frac{1}{2}ln|{x-2)}[/m]
[m]ln|v|=ln\sqrt{\frac{x-2}{x-4}}[/m]
[m]v=\sqrt{\frac{x-2}{x-4}}[/m]
и подставляем во второе
[m]u`\cdot\sqrt{\frac{x-2}{x-4}}=\sqrt{x-2}[/m]
[m]u`=\sqrt{x-4}[/m]
[m]u= ∫ \sqrt{x-4}dx[/m]
[m]u=\frac{(x-4)^{\frac{3}{2}}}{\frac{3}{2}}+C[/m]
[m]u=\frac{2}{3}\sqrt{(x-4)^3}+C[/m]
y=u*v
[m]y=(\frac{2}{3}\sqrt{(x-4)^3}+C)\cdot \sqrt{\frac{x-2}{x-4}}[/m]
