Задача 71123 неопределенный интеграл (x) / (x^3 +...
Условие
неопределенный интеграл
(x) / (x^3 + 1) dx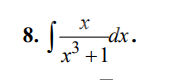
Решение
[m]x^3+1=(x+1)(x^2-x+1)[/m]
Раскладываем подынтегральную дробь на простейшие
[i]методом неопределенных коэффициентов[/i]:
[m] \frac{x}{x^3+1}=\frac{A}{x+1}+\frac{Mx+N}{x^2-x+1}[/m]
[m] x=A(x^2-x+1)+Mx^2+Nx+Mx+N[/m]
A+M=0
N-A+M=1
A+N=0
A=-1/3
M=N=1/3
[m] ∫ \frac{x}{x^3+1}dx= ∫\frac{(-\frac{1}{3})}{x+1}+\frac{\frac{1}{3}x+\frac{1}{3}}{x^2-x+1} =-\frac{1}{3} ∫ \frac{d(x+1)}{x+1}+\frac{1}{3}\cdot ∫\frac{(x+1)dx}{(x-\frac{1}{2})^2+\frac{3}{4}}[/m]
Замена переменной во втором интеграле:
[m]x-\frac{1}{2}=t[/m]
[m]dx=dt[/m]
[m]=-\frac{1}{3} ∫ \frac{d(x+1)}{x+1}+\frac{1}{3}\cdot ∫\frac{(t+\frac{1}{2}+1)dt}{t^2+\frac{3}{4}}=[/m]
[m]=-\frac{1}{3} ∫ \frac{d(x+1)}{x+1}+\frac{1}{3}\cdot ∫\frac{tdt}{t^2+\frac{3}{4}}+\frac{1}{3}\cdot \frac{3}{2}∫\frac{dt}{t^2+\frac{3}{4}}=[/m]
[m]=-\frac{1}{3}ln|x+1|+\frac{1}{6}ln|t^2+\frac{3}{4}|+\frac{1}{2\cdot \frac{\sqrt{3}}{2}}arctg\frac{t}{\frac{\sqrt{3}}{2}}+C[/m]
[m]=-\frac{1}{3}ln|x+1|+\frac{1}{6}ln|x^2-x+1|+\frac{1}{\sqrt{3}}arctg\frac{2x-1}{\sqrt{3}}+C[/m]
