Задача 70442 Вычислить объём тела, полученного...
Условие
математика ВУЗ
341
Решение
★
Выделяем полные квадраты
(x^2-2x)+(y^2-2y)=0
(x^2-2x+[b]1[/b])+(y^2-2y+[b]1[/b])=[b]2[/b]
(x-1)^2+(y-1)^2=2 - уравнение окружности с центром (1;1); R=sqrt(2)
Уравнение окружности состоит из двух ветвей
(x-1)^2=2-(y-1)^2
x-1= ± sqrt(2-(y-1)^2)
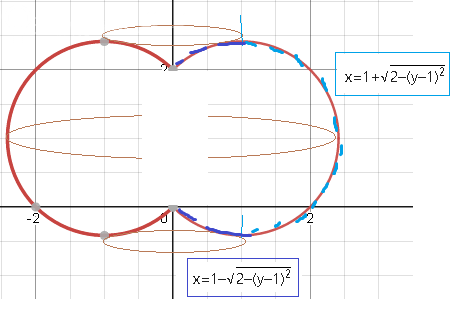
x=1+sqrt(2-(y-1)^2)
x=1-sqrt(2-(y-1)^2)
при x=1
y_(1)=1-sqrt(2) - наименьшее значение
y_(2)=1+sqrt(2) - наибольшее значение
[m]V=π ∫ _{1-\sqrt{2}}^{1+\sqrt{2}}(1+\sqrt(2-(y-1)^2))^2dy- π ∫^{0} _{1-\sqrt{2}}(1-\sqrt(2-(y-1)^2)^2dy -π ∫ _{2}^{1+\sqrt{2}}(1-\sqrt(2-(y-1)^2)^2dy=[/m]