Задача 70220 Хэлп…… Квадрат ABCD і прямокутник AB1C1D...

64171b8e080d9134f2688450

20.03.2023 10:03:37

Хэлп……
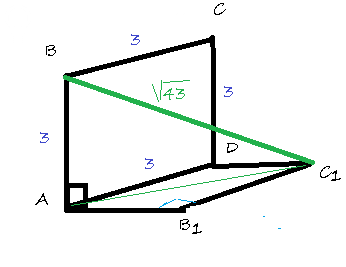
Квадрат ABCD і прямокутник AB1C1D зі спільною стороною AD лежать у двох перпендикулярних площинах. Знайдіть площу прямокутника, якщо площа квадрата дорівнює 9см^(2), а BC1 = sqrt(43) см

5f3ea7e3faf909182968ddd9

20.03.2023 12:05:19

★

S( квадрата) = a^2

S( квадрата) = 9 см2, значит, a^2=9
a=AB=AD = 3 см.


BC_(1) = √43 см

ΔABC_(1)-прямоугольный ( пл. АВСD ⊥ пл. АВ_(1)С_(1)D ⇒ АВ ⊥ пл. АВ_(1)С_(1)D ⇒ АВ перпендикулярна любой прямой в этой пл.
По теореме Пифагора:
AC^2_(1)=BC^2_(1)-AB^2=(\sqrt(43))^2-3^2=43-9=34

Δ АВ_(1)С_(1) - прямоугольный
По теореме Пифагора:
AB^2_(1)=AC^2_(1)-B_(1)C_(1)^2=(\sqrt(34))^2-3^2=34-9=25

Площадь прямоугольника:
S(пр) = AB_(1)*AD=5*3=15 см^2

626fab9a354ab65fb2f43abb

20.03.2023 11:26:02

Площадь квадрата:
S(кв) = AB^2 = 9 см^2, значит, AB = sqrt(9) = 3 см.
BC1 = sqrt(43) см
Площадь прямоугольника:
S(пр) = AB*B1 = 3*sqrt(43) см^2