Задача 70173 cos(2sinx + (1+sqrt(3))cosx) =...
Условие
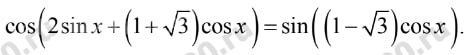
Решение
[m]cos α =sin β [/m] ⇒ [m]sin(\frac{π}{2}- α )=sin β [/m] ⇒ [m]sin(\frac{π}{2}- α )-sin β=0 [/m]
[m]2 sin \frac{(\frac{π}{2}- α )- β }{2} \cdot cos\frac{(\frac{π}{2}- α )+ β }{2}=0[/m]
[m] α =2sinx+(1+\sqrt{3})cosx[/m]
[m] β =(1-\sqrt{3})cosx[/m]
получаем:
[m]2 sin \frac{(\frac{π}{2}- 2sinx-(1+\sqrt{3})cosx )-(1-\sqrt{3})cosx }{2} \cdot cos\frac{(\frac{π}{2}- 2sinx-(1+\sqrt{3})cosx )+ (1-\sqrt{3})cosx }{2}=0[/m]
[m]2 sin (\frac{π}{4}- sinx-cosx) \cdot cos(\frac{π}{4}- sinx-\sqrt{3}cosx )=0[/m]
[m]sin (\frac{π}{4}- sinx-cosx)=0[/m] или [m] cos(\frac{π}{4}- sinx-\sqrt{3}cosx )=0[/m]
[m]\frac{π}{4}- sinx-cosx=πk, k ∈ [/m] [b]Z [/b] или [m] \frac{π}{4}- sinx-\sqrt{3}cosx=\frac{π}{2}+πn, n ∈ [/m][b]Z[/b]
[m]sinx+cosx=\frac{π}{4}+πm, m ∈ [/m] m=-k; [b]Z [/b] или [m]sinx+\sqrt{3}cosx=-\frac{π}{2} +\frac{π}{4} +πs, s ∈ [/m][b]Z[/b]s=-n
[m]sinx+cosx=\frac{π}{4}+πm, m ∈ [/m] [b]Z [/b] или [m]sinx+\sqrt{3}cosx=-\frac{π}{2} +\frac{π}{4} +πs, s ∈ [/m][b]Z[/b]
[m]\sqrt{2}\cdot sin(\frac{π}{4}+x)=\frac{π}{4}+πm, m ∈ [/m] [b]Z [/b] или [m]2sin(\frac{π}{3}+x)=-\frac{π}{4} +πs, s ∈ [/m][b]Z[/b]
В силу ограниченности синуса уравнения имеют решения только в случае
[m]-\sqrt{2} ≤ \frac{π}{4}+πm ≤\sqrt{2} , m ∈ [/m] [b]Z [/b] или [m]-2≤ -\frac{π}{4}+πs ≤2 , s ∈ [/m] [b]Z [/b]
т.е
при m=0 или при s=0
Решаем [i]простейшие тригонометрические уравнения [/i]:
[m]\sqrt{2}\cdot sin(\frac{π}{4}+x)=\frac{π}{4} [/m] или [m]2\cdot sin(\frac{π}{3}+x)=-\frac{π}{4} [/m]
[m] sin(\frac{π}{4}+x)=\frac{π}{4\sqrt{2}} [/m] или [m]sin(\frac{π}{3}+x)=-\frac{π}{8} [/m]
[m] \frac{π}{4}+x=(-1)^{k}arcsin \frac{π}{4\sqrt{2}}+πk, k ∈ [/m] [b]Z[/b] или [m]\frac{π}{3}+x=(-1)^{n}arcsin(-\frac{π}{8})+πn, n ∈ [/m][b]Z[/b]
[m]x=(-1)^{k}arcsin \frac{π}{4\sqrt{2}}-\frac{π}{4}+πk, k ∈ [/m] [b]Z[/b] или [m]x=(-1)^{n}arcsin(-\frac{π}{8})-\frac{π}{3}+πn, n ∈ [/m][b]Z[/b]
О т в е т.
[m](-1)^{k}arcsin \frac{π}{4\sqrt{2}}-\frac{π}{4}+πk, k ∈ [/m] [b]Z[/b] ; [m](-1)^{n}arcsin(-\frac{π}{8})-\frac{π}{3}+πn, n ∈ [/m][b]Z[/b]