Задача 69854 Прямокутник АВСЕ перегнули по діагоналі...

6405f711761fa777e0fe1b73

06.03.2023 17:23:12

Прямокутник АВСЕ перегнули по діагоналі ВЕ так що площини АВЕ та
СВЕ виявилися перпендикулярними. Знайдіть відстань між точками А і С ,
якщо менша із сторін прямокутника дорівнює 6 см, а кут між його діагоналями
60

5f3ea7e3faf909182968ddd9

06.03.2023 17:54:27

★

рис. 1
ABCD – прямоугольник,
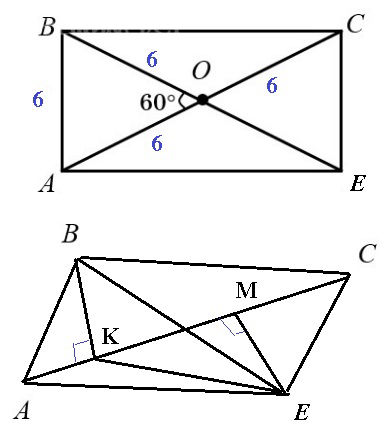
AB = 6 см, ∠AOB = 60°


Δ AOB – равнобедренный с углом 60° при вершине.
Значит Δ AOB - равносторонний

АО = ВО =6 см

Диагонали прямоугольника
АС = BD = 12

рис. 2

(ABC) ⊥ (AEC),

Проводим
ВК⊥ AC
EM⊥ AC
ВК - высота равностороннего Δ AOB
ВК=ЕМ=6sqrt(3)/2=3sqrt(3)

По теореме Пифагора
AK^2=6^2-(3sqrt(3)^2=36-27=9
AK=MC=3
КМ=АС-АК-МС=12-3-3=6

Δ КМЕ
По теореме Пифагора
КЕ^2=KM^2+EM^2=6^2+(3sqrt(3))^2=36+27=65

(ABC) ⊥ (AEC) ⇒

ΔBКE

∠BКE = 90 °
По теореме Пифагора
BE^2=BK^2+KE^2=(3sqrt(3))^2+65=27+65=92

[b]BE=sqrt(92)[/b]