Задача 68991 Исследовать функцию с помощью...
Условие
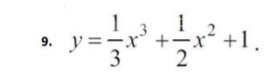
Решение
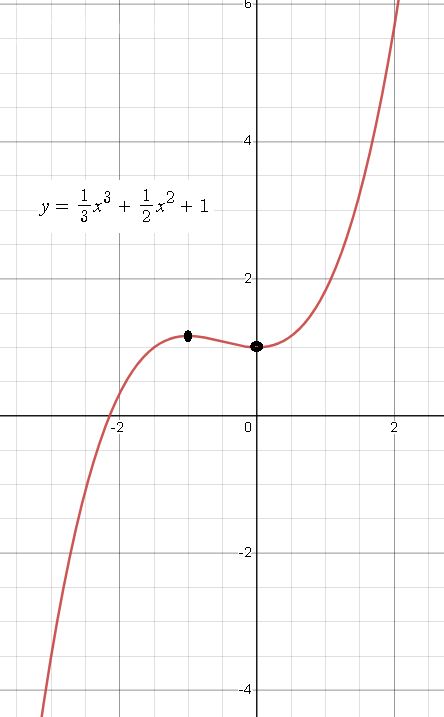
Исследование функции с помощью производной:
y`=(1/3)x^3+(1/2)x^2+1)`
y`=(1/3)*3x^2+(1/2)*2x^2
y`=x^2+x
y`=0
x^2+x=0
x=-1; x=0
Расставляем знак производной
_+__ (-1) __-___ (0) __+__
х=-1 - точка максимума, производная меняет знак с + на -
х=0 - точка минимума, производная меняет знак с - на +
y(-1)=-(1/3)+(1/2)+1=[b]7/6[/b]
y(0)=[b]1[/b]
y`> 0 на (- ∞ ;-1) и на (0;+ ∞ )
Функция возрастает на (- ∞ ;-1) и на (0;+ ∞ )
y`<0 на (-1;0)
Функция убывает на (-1;0)
Исследование функции с помощью второй производной:
y``=(y`)`=(x^2+x)`=2x+1
y``=0
2x+1=0
x=-1/2 - точка перегиба, вторая производная меняет знак
y``<0 на (- ∞ ;-1/2) ⇒ кривая выпукла вверх ( ∩ ) на (- ∞ ;-1/2)
y`>`0 на (-1/2;+ ∞ ) ⇒ кривая выпукла вниз ( ∪ ) на (-1/2;+ ∞ )