Задача 68782 Средняя линия прямоугольной трапеции...

63d7bb5b939a43299dd1139a

30.01.2023 15:52:05

Средняя линия прямоугольной трапеции равна 6.

5f3ea7e3faf909182968ddd9

30.01.2023 17:32:39

★

Так как расстояния от точки M до сторон трапеции равны, то OM ⊥ пл АВСD ⇒
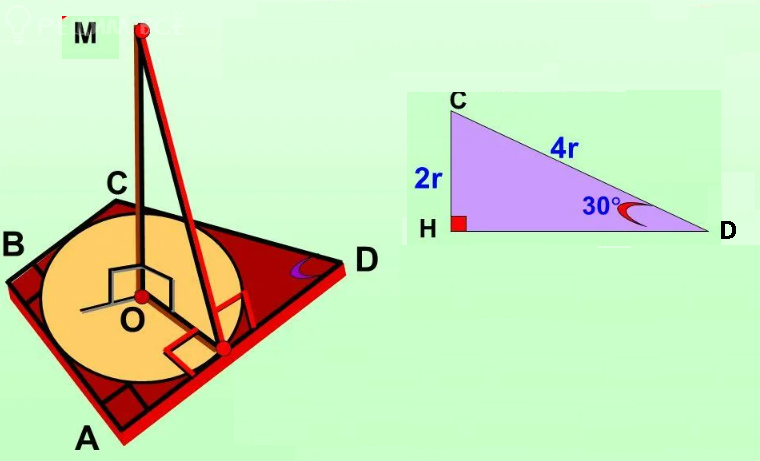
O-центр вписанной окружности

AB+CD=BC+AD

m=(a+b)/2 ⇒ a+b=12

BC+AD=12
AB+CD=12

Проводим высоту из точки С:
СН=2r
⇒
CD=4r

CH=AB

2r+4r=12
6r=12
[b]r=2[/b]

ОК=r

MK^2=MO^2+OK^2=(2sqrt(3))^2+2^2=12+4=16

MK=[b]4[/b]