Задача 68650 Найти область сходимости ряда...
Условие
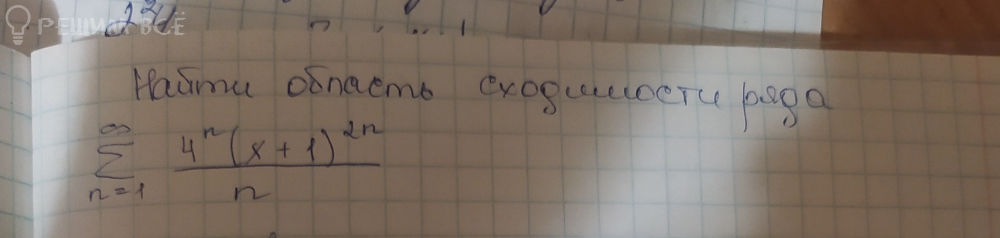
Решение
[m]lim_{n → ∞ }\frac{\frac{4^{n+1}\cdot |x+1|^{2(n+1)}}{n+1}}{\frac{4^{n}\cdot |x+1|^{2n}}{n}}=[/m]
[m]=4\cdot |x+1|^2\cdot lim_{n → ∞ }\frac{n+1}{n}=4\cdot |x+1|^2\cdot 1=4\cdot |x+1|^2[/m]
По признаку Даламбера данный ряд сходится и притом абсолютно, если
[m]4\cdot |x+1|^2<1[/m] ⇒
[m]|x+1|^2<\frac{1}{4}[/m]
[m]|x+1|<\frac{1}{2}[/m]
[m]-\frac{1}{2}<x+1<\frac{1}{2}[/m]
[m]-\frac{3}{2}<x<\frac{1}{2}[/m]
Проверяем сходимость на концах интервала:
[m]x=-\frac{3}{2}[/m]
Получаем числовой ряд
[m]∑_{n=1}^{ ∞ }\frac{4^{n}\cdot (-\frac{1}{2})^{2n}}{n}[/m]
[m]∑_{n=1}^{ ∞ }\frac{1}{ n}[/m]
Ряд [b]расходится[/b], потому что это [i]гармонический [/i]ряд.
[m]x=\frac{1}{2}[/m]
Получаем числовой ряд
[m]∑_{n=1}^{ ∞ }\frac{4^{n}\cdot (\frac{3}{2})^{2n}}{n}[/m]
[m]∑_{n=1}^{ ∞ }\frac{9^{n}}{ n}[/m]
Ряд[b] расходится[/b] по признаку Даламбера
[m]lim_{n → ∞ }\frac{\frac{9^{n+1}}{n+1}}{\frac{9^{n}}{n}=9 > 1[/m]
О т в е т. [m](-\frac{3}{2};\frac{1}{2})[/m]