Задача 68616 1 Дано: DА перпендикулярно (ABC), <BAC =...

63c6fa089d70ba753414d60e

24.01.2023 20:50:31

1
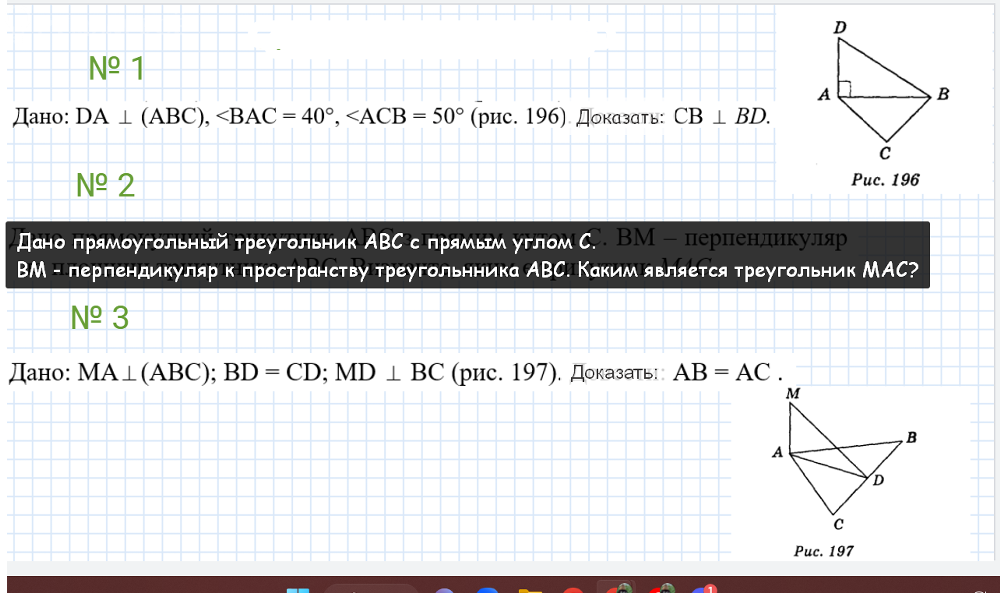
Дано: DА перпендикулярно (ABC), <BAC = 40°, <ACB = 50° (рис. 196) Доказать: СВ перпендикулярно BD.

№ 2
Дано прямоугольный треугольник с прямым углом
ВМ - перпендикуляр к пространству треугольнника АВС. Каким является треугольник МАС?

№3
...

5f3ea7e3faf909182968ddd9

25.01.2023 11:47:03

★

[b]1.[/b]
Сумма углов треугольника АВС равна 180 °
∠ ВАС+ ∠ АСВ+ ∠ АВС=180 °
∠ ВАС=40 °
∠ АСВ=50 °
∠ АВС=180 ° -40 ° -50 °
∠ АВС=90 ° ⇒ СВ ⊥ АВ

AD ⊥ плоскости АВС ⇒АВ ⊥ любой прямой, лежащей в плоскости АВС ⇒
AD ⊥ CB

СВ ⊥ АВ
СВ ⊥ АD
CB ⊥ двум пересекающимся прямым плоскости ABD ⇒ CВ ⊥ любой прямой, лежащей в плоскости ABD

⇒ [b]CВ ⊥ BD[/b]

[b]3.[/b]

MD ⊥ BC⇒ MD- высота
BD=CD ⇒ MD- медиана
⇒ MD- медиана и высота
⇒ Δ ВМС - [i]равнобедренный[/i]

BM=CM

MA ⊥ плоскости АВС

АС - проекция MС
AB- проекция MB

[i]Равные [/i]наклонные имеют [i]равные[/i] проекции
⇒
АВ=АС


[b]2.[/b]
ВМ ⊥ плоскости АВС⇒ВМ ⊥ любой прямой, лежащей в плоскости АВС

BM ⊥ BC

⇒ BC - проекция MC



Δ АВС - прямоугольный

BC ⊥ AC

BC - проекция MC ⇒ BC⊥ АC наклонная MC ⊥ AC ⇒ ΔACM- прямоугольный