Задача 68538 Используя признак Даламбера, определите...
Условие
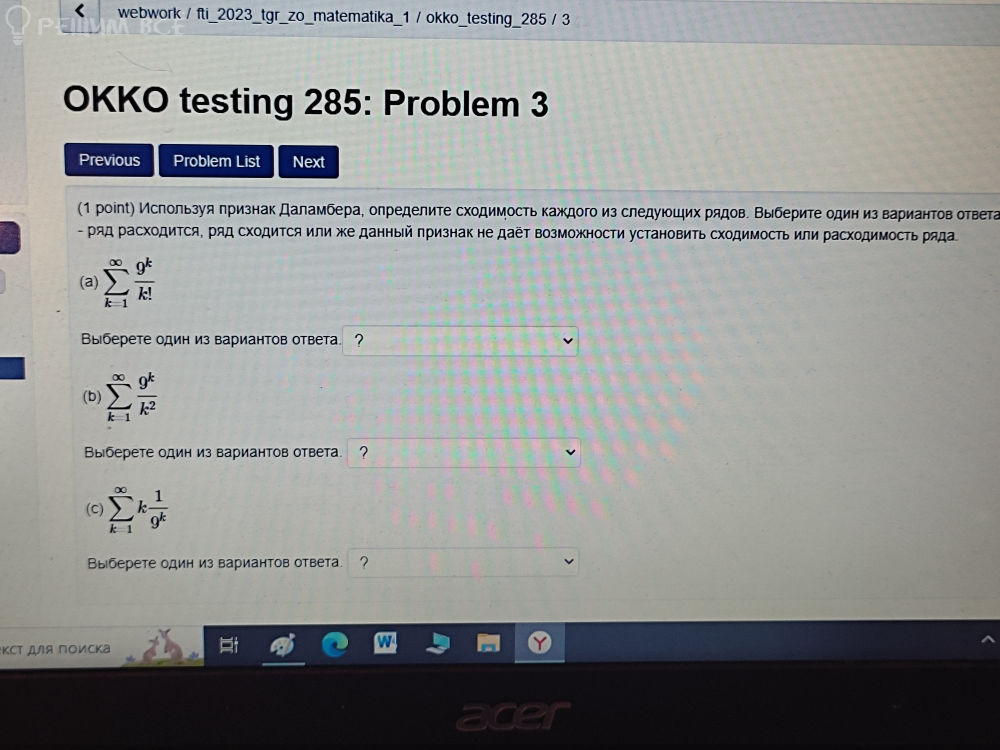
Решение
Ряд[b] сходится[/b] по признаку Даламбера
[m]lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{9^{n+1}}{(n+1)!}}{\frac{9^{n}}{n!}}=9 lim_{n → ∞ }\frac{1}{n}=0<1[/m]
b)
Ряд [b]расходится [/b]по признаку Даламбера
[m]lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{9^{n+1}}{(n+1)^2}}{\frac{9^{n}}{n^2}}=9\cdot lim_{n → ∞ }\frac{n^2}{(n+1)^2}=9\cdot 1=9>1[/m]
c)
Ряд [b]сходится[/b] по признаку Даламбера
[m]lim_{n → ∞ } \frac{a_{n+1}}{a_{n}}=lim_{n → ∞ }\frac{\frac{n+1}{9^{n+1}}}{\frac{n}{9^{n}}}=\frac{1}{9}lim_{n → ∞ }\frac{n+1}{n}=\frac{1}{9}\cdot 1=\frac{1}{9}<1[/m]