Задача 68120 Вокруг оси Ох фигуры, ограниченной...

63b89456338a47227b6e5f27

07.01.2023 00:37:21

Вокруг оси Ох фигуры, ограниченной линиями снизу

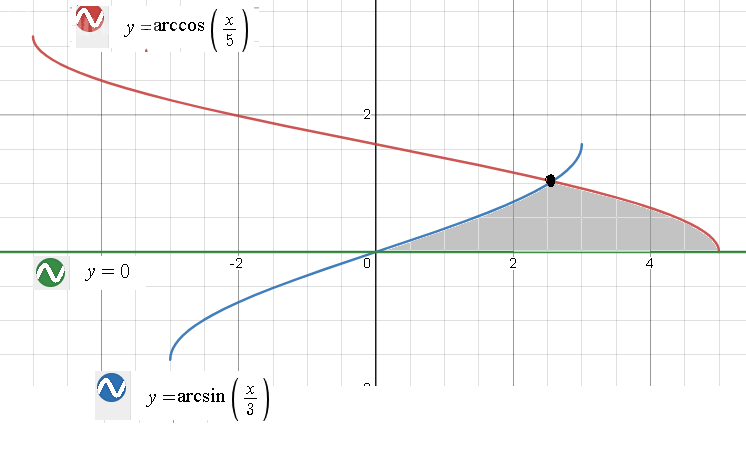
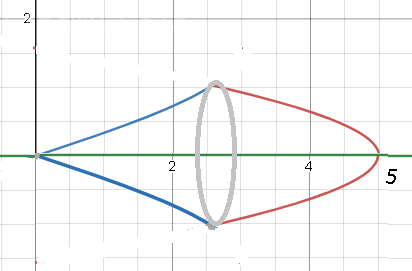
найти объем тела, образованного вращением.

y = arccos (x/5), y = arcsir (x/3), y = 0

5f3ea7e3faf909182968ddd9

07.01.2023 10:30:13

★

Область определения [m]y=arccos\frac{x}{5}[/m]

[m]-1 ≤ \frac{x}{5} ≤ 1[/m]

[m]-5 ≤x ≤ 5[/m]


Область определения [m]y=arcsin\frac{x}{3}[/m]

[m]-1 ≤ \frac{x}{3} ≤ 1[/m]

[m]-3 ≤x ≤ 3[/m]


Рассматриваем криволинейную трапецию на [0;5]


Находим координаты точки пересечения графиков

[m]y=arccos\frac{x}{5}[/m] и [m] y=arcsin\frac{x}{3}[/m]


[m]arccos\frac{x}{5}=arcsin\frac{x}{3}[/m]


⇒ [m]cosy=\frac{x}{5}=[/m] и [m] sin y=\frac{x}{3}[/m]


⇒ [m]x=5cosy[/m] и [m]x=3siny[/m]

Поэтому


[m]5cosy=3siny[/m]- однородное тригонометрическое уравнение первой степени.

Делим на [m]cosy ≠0 [/m]

[blue][m]tgy=\frac{5}{3}[/m][/blue]



[m]1+tg^2y=\frac{1}{cos^2y}[/m] ⇒ [m]1+(\frac{5}{3})^2=\frac{1}{cos^2y}[/m]

[m]cos^2y=\frac{9}{34}[/m]



[m]cosy=\frac{3}{\sqrt{34}}[/m]

тогда

[m]arccos\frac{x}{5}=arccos\frac{3}{\sqrt{34}}[/m] ⇒

[m]\frac{x}{5}=\frac{3}{\sqrt{34}}[/m]

[m]x=\frac{15}{\sqrt{34}}[/m]



[m]V_{Ox}=π ∫ _{0}^{\frac{15}{\sqrt{34}}}arccos^2(\frac{x}{5})dx+π ∫ _{\frac{15}{\sqrt{34}}}^{5}arcsin^2(\frac{x}{3})dx=[/m]


Применить метод интегрирования по частям