Задача 68085 В небольшом магазине работают два...
Условие
Решение
Пусть событие А - "работает Игорь"; событие В-" работает Юрий".
Изображаем кругами Эйлера ( синий круг - вероятность работы Игоря, красный - вероятность работы Юрия)
События совместны, пересечение кругов :
событие (А ∩ B) - " одновременная работа и Игоря и Юрия"
По условию эта вероятность равна 0,2
p(A ∩ B)=0,2
Тогда событие
(A\B)- "работает только Игорь" ( на рис. голубой цвет)
(В\A)- "работает только Юрий"( на рис. розовый цвет)
Обозначим p(A\B)=p(B\A)= [b]х[/b]- вероятность того, что работает только один
Тогда
p(A)=(х+0,2) - вероятность того, что работает Игорь, один или одновременно с Юрием
p(B)=(х+0,2) - вероятность того, что работает Юрий, один или одновременно с Игорем
Тогда
событие C= A ∪ B- " работает хотя бы один "
События совместны, поэтому
p(C)=p(A)+p(B)-p(A ∩B)=(x+0,2)+(x+0,2)-0,2 - вероятность того, что работает хотя бы один
Тогда противоположное событие
vector{C}-" оба свободны"
По условию вероятность p(vector{C})=0,25
p(C)+p( vector{C})=1
Значит
(x+0,2)+(x+0,2)-0,2+0,25=1 ⇒
2x=0,55
x=0,275
О т в е т. 0,[b]275[/b]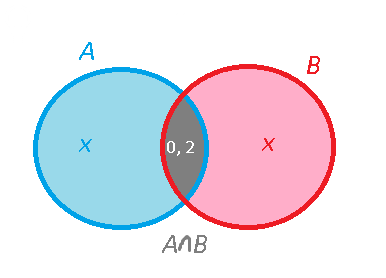
Все решения