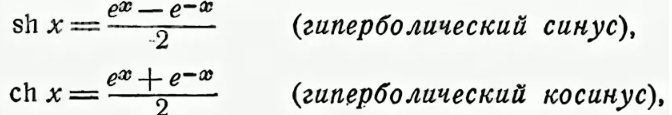Задача 67738 Используя первые четыре члена разложения...

637921394cfcd5727962e7cc

20.12.2022 20:15:44

Используя первые четыре члена разложения по формуле Тейлора, вычислить приближенно : ch(1.04) = (e^(1.04 )- e^(-1.04))/2

5f3ea7e3faf909182968ddd9

20.12.2022 21:02:55

★

Так как разложение y=e^(x) в ряд имеет вид:

[m]e^{x}=1+x+\frac{x^2}{2}+\frac{x^3}{3!}+...[/m]

то

[m]e^{1,04} ≈ 1+1,04+\frac{1,04^2}{2}+\frac{1,04^3}{3!}[/m]

[m]e^{-1,04} ≈ 1-1,04+\frac{(-1,04)^2}{2}+\frac{(-1,04)^3}{3!}[/m]


[m]ch1,04 = \frac{e^{1,04}+e^{-1,04}}{2}[/m]

[m]ch1,04 ≈ \frac{1+1,04+\frac{1,04^2}{2}+\frac{1,04^3}{3!}+(1-1,04+\frac{(-1,04)^2}{2}+\frac{(-1,04)^3}{3!})}{2}=\frac{2+1,04^2}{2}=\frac{2+1,0816}{2}=1,5408[/m]