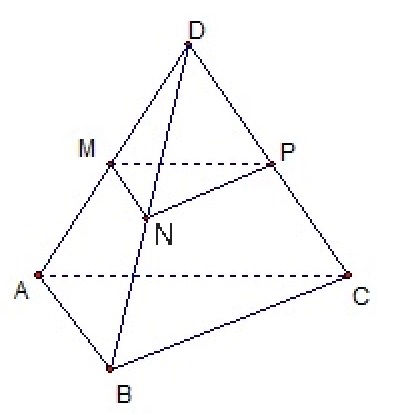
Задача 67317 В тетраэдре ABCD точки М,N и P является...

638a6b654b112844a67b7603

03.12.2022 18:06:50

В тетраэдре ABCD точки М,N и P является серединами ребер AD и BD и CD. Найдите площадь сечения MNP, если площадь грани ABC равна 20.

5f3ea7e3faf909182968ddd9

03.12.2022 21:26:07

★

MN - средняя линия Δ ADB ⇒ MN || AB

Аналогично
NP ||BC
MP|| AC

∠ PMN= ∠ CAB как углы с соответственно параллельными сторонами

∠ MNР= ∠ ABС как углы с соответственно параллельными сторонами

Δ ABC ∼ Δ MNP по двум углам


[red][b]k=2 [/b]
[/red]
Так как
MN - средняя линия Δ ADB ⇒ MN =(1/2)| AB ⇒

AB=[red]2[/red]MN


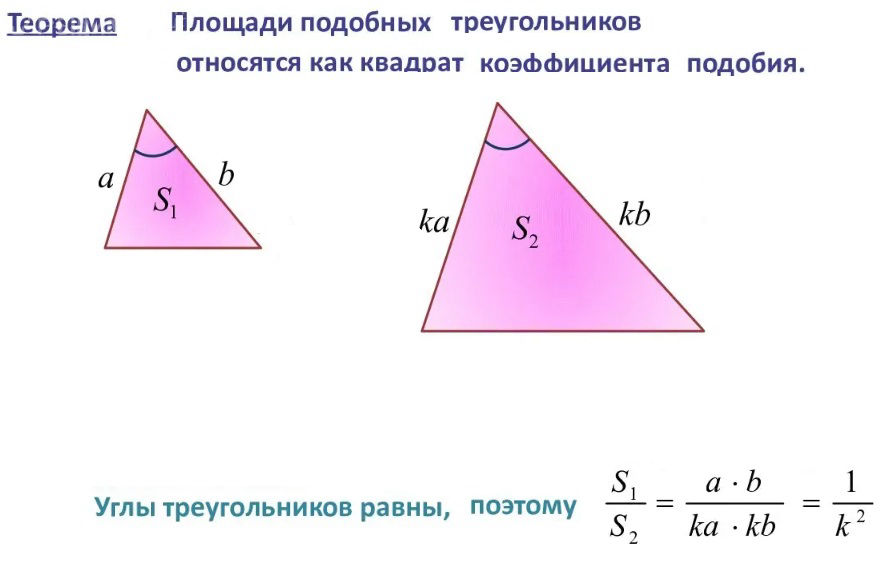
Cм скрин

S_( Δ ABC):S_( Δ MNP)=k^2

k=2, так как точки М,N и P является[b] серединами[/b] ребер AD и BD и CD.


S_( Δ ABC):S_( Δ MNP)=2^2 ⇒ S_( Δ MNP)=S_( Δ ABC):4=20:4=[red]5[/red]CFB