Задача 66834 подробно прошу. если что это производные...
Условие
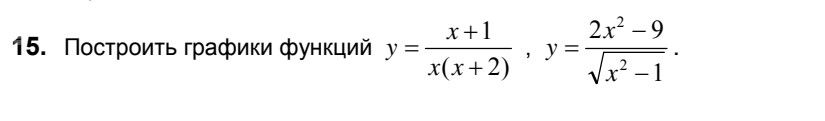
Решение
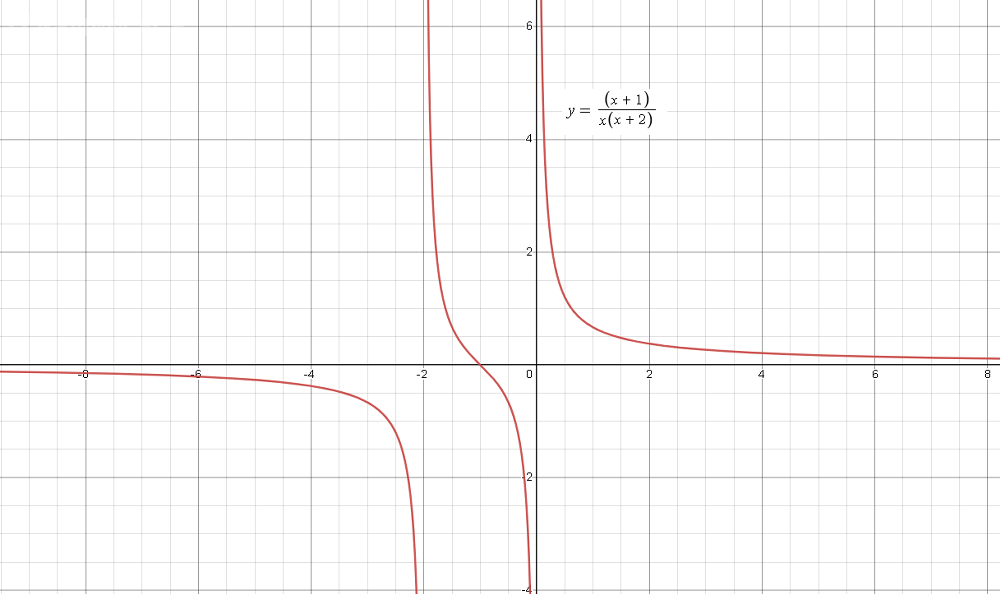
Область определения: x(x+2) ≠ 0 ⇒ x ≠ 0; x ≠-20
[b](- ∞ ;-2) U (-2;0) U(0;+ ∞ )[/b]
x= -2 - вертикальная асимптота, так как
lim_(x → [b]-2[/b])f(x)=[b] ∞[/b]
x= 0 - вертикальная асимптота, так как
lim_(x → [b]0[/b])f(x)=[b] ∞[/b]
y=0 - горизонтальная асимптота , так как
lim_(x → ∞ )f(x)= [b]0[/b]
Исследование с помощью первой производной
y`= ((x+1)`*x*(x+2)-(x+1)*(x*(x+2))`)/(x^2*(х+2)^2)
y`=(-x^2-2x-2)/(x^2*(х+2)^2)
y`>0
Функция монотонно [i]убывает [/i]
на (- ∞ ;-2) и на (-2;0) и на (0;+ ∞ )
и не имеет экстремумов
y``=[b]([/b](-x^2-2x-2)`*x^2*(х+2)^2-(-x^2-2x-2)*(x^2*(х+2)^2)`[b])[/b]/(x^4*(х+2)^4)
y``=[b]([/b](-2x-2)*x^2*(x+2)^2+(x^2+2x+2)*(4x^3+6x^2+4x)[b])[/b]/(x^4*(х+2)^4)
y``=0
x= -1 [i] точка перегиба.[/i]
2.
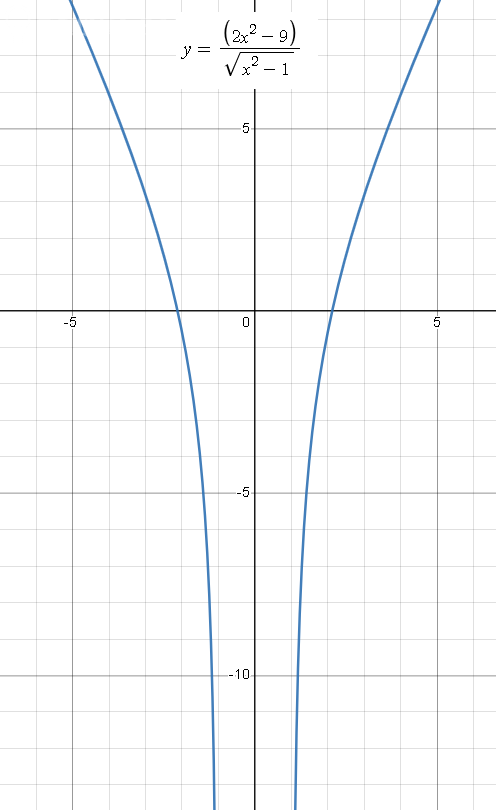
Область определения:
(x^2-1)> 0 ⇒
[b](- ∞ ;-1) U(1;+ ∞ )[/b]
x= -1 - вертикальная асимптота, так как
lim_(x → [b]-1[/b])f(x)=[b] ∞[/b]
x=1 - вертикальная асимптота, так как
lim_(x → [b]1[/b])f(x)=[b] ∞[/b]
Горизонтальных асимптот нет , так как
lim_(x → ∞ )f(x)= [b] ∞ [/b]
Исследование с помощью первой производной
y`= ((2x^2-9)`*sqrt(x^2-1)-(2x^2-9)*(sqrt(x^2-1))`)/(sqrt(x^2-1))
y`=x*(4x^2-4-2x^2+9)/((x^2-1)sqrt(x^2-1))
y`=x(2x^2+9)/((x^2-1)sqrt(x^2-1))
y`=0
x=0 - не является точкой возможного экстремума, так как 0 ∉ [b](- ∞ ;-1) U(1;+ ∞ )[/b]
y` < 0 на (- ∞ ;-1)
Функция монотонно [i]убывает [/i] на (- ∞ ;-1)
y`>0 на (1;+ ∞ )
Функция монотонно [i]возрастает [/i] на (1;+ ∞ )
И не имеет экстремумов