Задача 66713 ...

6342adef2ffdf102e7335cc0

06.11.2022 15:17:52

Решит® урзвнения: А) loga(6X— 9) = 2 5) \ова2(5Х — 10)= -2 Решите цсравойства: A)logoz(5¢~ 15) < -2 S] logo “ 2-1 Решуте трафическя уразнение 10805 ®"* 3 Расставьте числЭ 2,0.6% 8 поряди® убылания если * 03>, вв1‚2"’р\‹\;‚‚256. ye=(loRo, 8)?

5f3ea7e3faf909182968ddd9

06.11.2022 16:43:48

★

1)
А)
По определению логарифма
6x-8=4^2
6x=16+8
6x=24
x=4
Проверка:
log_(4)(6*4-8)=log_(4)16=2
2=2- верно
x=4 - корень уравнения

О т в е т. 4

Б)
По определению логарифма
5х-2=0,2^(-2)
0,2=1/5=5^(-1)
5х=5^2+2
5х=27
х=5,4
Проверка:
log_(0,2)(5*5,4-2)=log_(0,2)25=-2
-2=-2- верно
x=5,4 - корень уравнения

О т в е т. 5,4


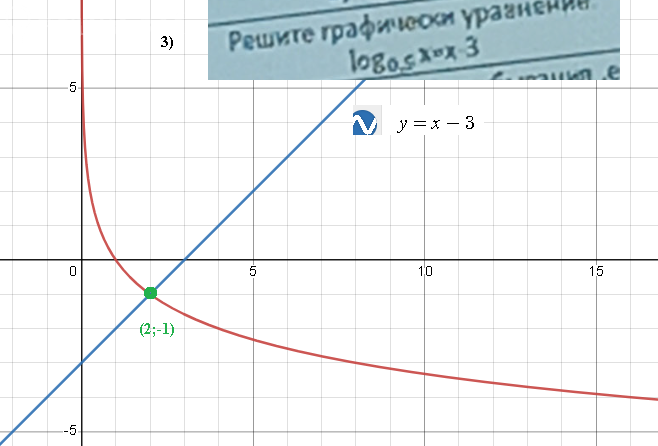
2)
A)
В неравенстве проверить ответ не получится, поэтому решают неравенства с нахождением [b]о[/b]бласти [b]д[/b]опустимых [b]з[/b]начений переменной, входящей в уравнение ( сокращенно ОДЗ)

ОДЗ:
5х-15 >0 ⇒ [red]x > 3[/red]

Так как
-2=log_(0,2)25, то неравенство можно записать в виде:

log_(0,2)(5x-15) ≤ log_(0,2)25

Логарифмическая функция с основанием [b]0 < 0,2 < 1[/b] [i]убывающая[/i], поэтому переходим от логарифмов к неравенству с аргументами и МЕНЯЕМ ЗНАК НЕРАВЕНСТВА

(5x-15) ≥ 25
5х ≥ 40
[b]х ≥ 8[/b]


С учетом ОДЗ
{[red]x > 3[/red]
{[b]х ≥ 8[/b]

О т в е т. [8;+ ∞ )

Б)
{[red]x >0[/red]
{log_(0,6)x ≥ log_(0,6)0,6^(-1) ⇒

{[red]x >0[/red]
{x ≤ 0,6^(-1)

{[red]x >0[/red]
{x ≤ 5/3

О т в е т. (0; 5/3]



4)
a=0,3^(-3)=(10/3)^3=1000/27

b=1,2^(-3)=((12/10)^(-1))^3=(10/12)^(3)=1000/(144*12)< a

c=log_(4)256=4, так как 4^4=16^2=256

k=(log_(0,5)8)^3=-3^(3)=-27

[b]c > b > a > k[/b]