Задача 66666 Определить характер точек разрыва...
Условие
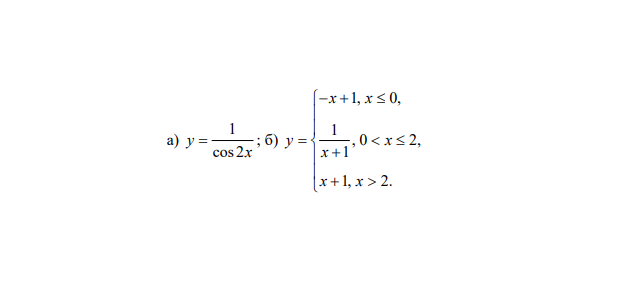
Решение
Область определения:
cos2x ≠ 0 ⇒
2x ≠ (π/2)+πk, k ∈ Z
x≠ (π/4)+(π/2)k, k ∈ Z
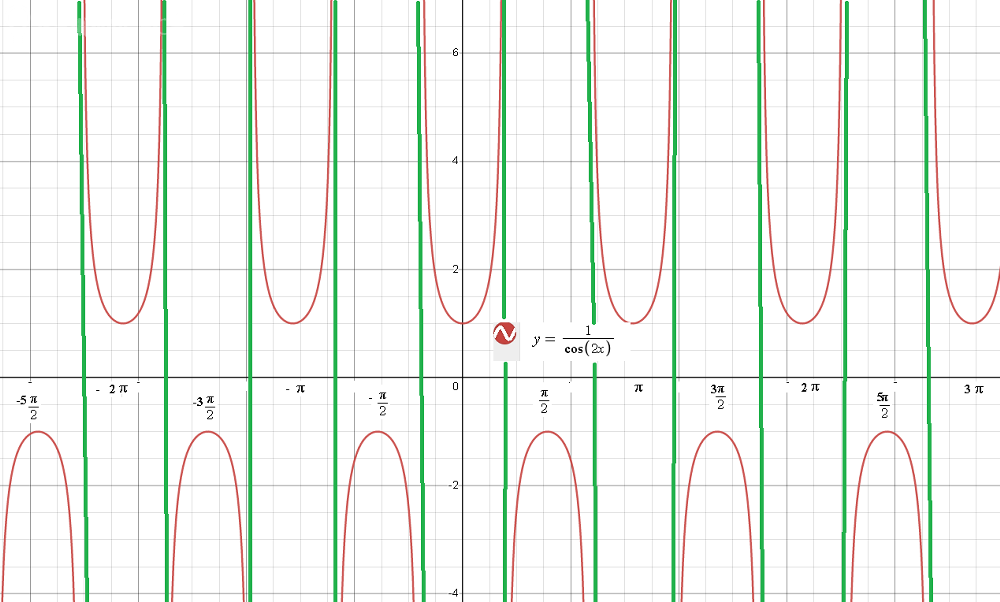
Прямые x= (π/4)+(π/2)k, k ∈ Z- [i]вертикальные асимптоты[/i], так как
[m]lim_{x → (π/4)+(π/2)k, k ∈ Z}\frac{1}{cos2x}= ∞ [/m]
[m]y`=\frac{1}{cos^22x}\cdot (cos2x)`[/m]
[m]y`=\frac{-sin2x\cdot (2x)`}{cos^22x}[/m]
[m]y`=\frac{-2sin2x}{cos^22x}[/m]
y`=0
sin2x=0
2x=πn, n ∈ Z
x=(π/2) n, n ∈ Z - точки возможных экстремумов..
x=(π/2)*(2m+1), m∈ Z - точки максимумов
x=(π/2)*(2m), m∈ Z - точки минимумов
2.
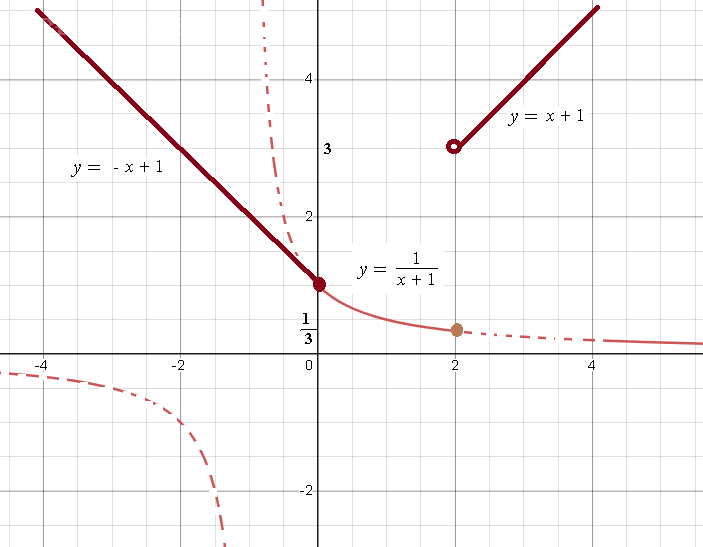
На (- ∞ ;0) функция непрерывна, так как y=-х+1 непрерывна на (- ∞ ;+ ∞ )
На (0;2) функция непрерывна, так как y=1/(x+1) непрерывна на (- ∞ ;+ ∞ )
На (2;+ ∞ ) функция непрерывна, так как y=x+1 непрерывна на (- ∞ ;+ ∞ )
Значит, надо выяснить непрерывность функции в точках
х=0 и х=2
Находим предел слева:
lim_(x → -0)f(x)=lim_(x → -0)(-x+1)=1
Находим предел справа:
lim_(x → +0)f(x)=lim_(x → 2+0)(1/(x+1))=1
Предел слева равен пределу справа, значит функция имеет предел в точке
Значение функции в точке равно пределу
х=0 - [i]точка непрерывности[/i]
x=2
Находим предел слева:
lim_(x →2 -0)f(x)=lim_(x → 2-0)1/(х+1)=1/3
Находим предел справа:
lim_(x →2 +0)f(x)=lim_(x → 2+0)(x+1)=3
х=2 - [i]точка разрыва первого рода [/i]
предел слева ≠ пределу справа , значит функция не имеет предела в точке
х=2 - [i]точка разрыва первого рода [/i]