Задача 66557 Интеграл. Вычислить площадь плоской...
Условие
Интеграл. Вычислить площадь плоской фигуры, ограниченной линиями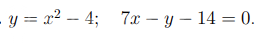
математика ВУЗ
378
Решение
★
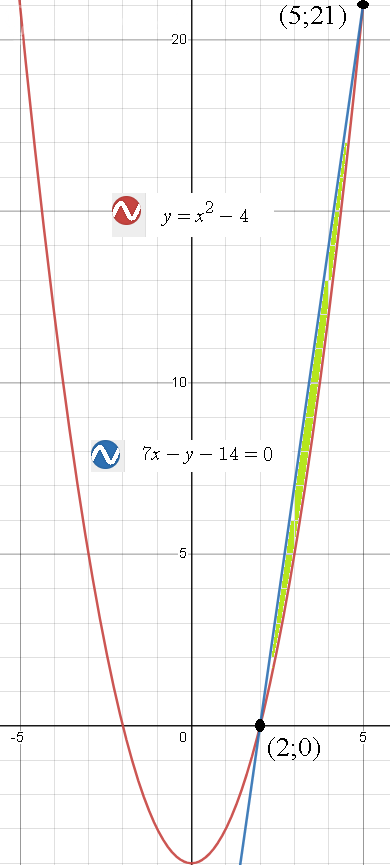
y=7x-14 - прямая
См. рис.
Находим абсциссы точек пересечения
x^2-4=7x-14
x^2-7x+10=0
x_(1)=[b]2[/b]; x_(2)=[b]5[/b]
g(x)=7x-14
f(x)=x^2-4
По правилу см. скрин
[m]S= ∫ _{2}^{5}(7x-14-(x^2-4))dx= ∫ _{2}^{5}(7x-14-x^2+4)dx= ∫ _{2}^{5}(7x-x^2-10)=(7\frac{x^2}{2}-\frac{x^3}{3}-10x)| _{2}^{5}=[/m]
[m]=(7\frac{5^2}{2}-\frac{5^3}{3}-10\cdot 5)-(7\frac{2^2}{2}-\frac{2^3}{3}-10\cdot 2)=...[/m] считайте