Задача 66550 ...

635b93c21e7292260877bd3b

28.10.2022 11:37:53

Прямые а и в пересекаются в точке М. Плоскости а и в параллельны. Прямая a пересекает плоскость а в точке A, а плоскость β в точке В. Прямая b пересекает плоскость а в точке С, а плоскость В в точке D.
AM/AB=2/3. Найдите MC/CD

5f3ea7e3faf909182968ddd9

28.10.2022 18:57:52

★

1 случай:
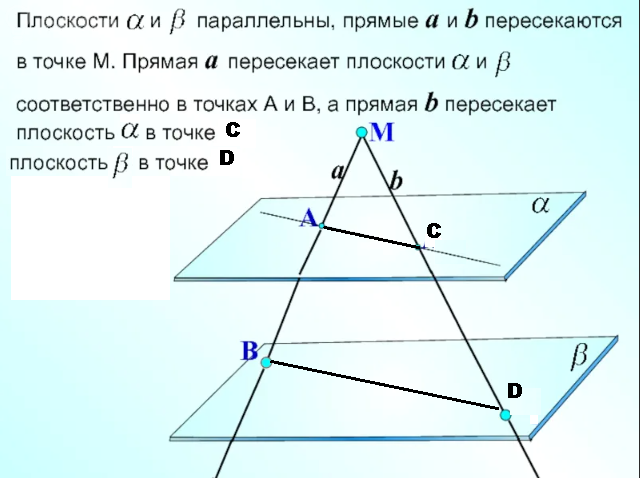
(cм. рис. 1)
Через две пересекающиеся прямые a и b проходит плоскость и при том только одна.

Эта плоскость пересекает параллельные плоскости по двум параллельным прямым:

АС || BD

Значит
Δ AMC ∼ Δ BMD

Из подобия

АМ: BM=CM:DM

По условию

АМ: АВ=2:3 ⇒ АM=2x; AB=3x

BM=BA+AM=3x+2x=5x

АМ: BM=2x:5x=2:5 ⇒

CM:DM=2:5

CM=2y
DM=5y

CD=5y-2y=3y

МС:CD=2y:3y=[b]2:3[/b]


2 случай

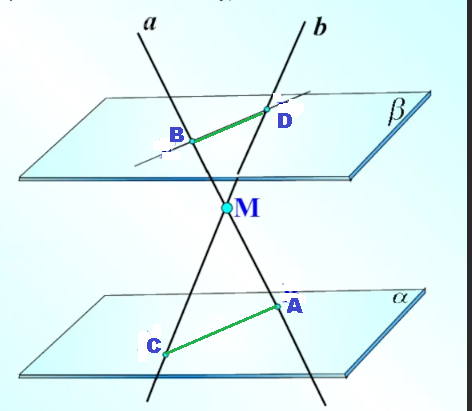
( см. рис. 2)

Через две пересекающиеся прямые a и b проходит плоскость и при том только одна.

Эта плоскость пересекает параллельные плоскости по двум параллельным прямым:

АС || BD

Значит
Δ AMC ∼ Δ BMD

Из подобия

АМ: BM=CM:DM

По условию

АМ: АВ=2:3 ⇒ АM=2x; AB=3x

BM=AB-AM=3x-2x=x

АМ: BM=2:1

⇒
CM:DM=2:1

CM=2y
DM=y

CD=CM+MD=2y+y=3y

CM:CD=2y:3y=[b]2:3[/b]