Задача 66526 Нужно решить 6 пример по формулам...
Условие

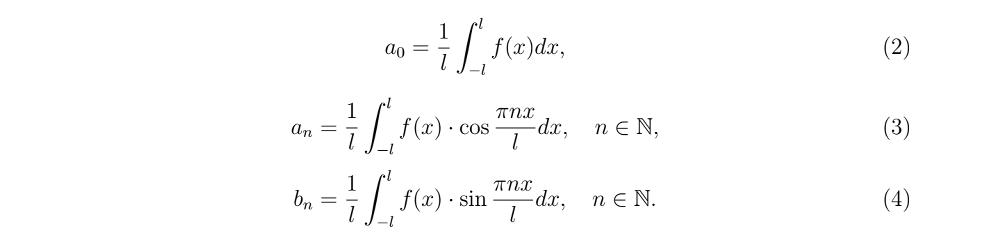
Решение
[m] l=π[/m]
[m]a_{o}=\frac{1}{π} ∫_{-π} ^{π}f(x)dx=\frac{1}{π} ∫_{-π} ^{0}(2x+3)dx+\frac{1}{π} ∫_{0} ^{π}(0)dx=[/m]
[m]a_{n}=\frac{1}{π} ∫_{-π} ^{π}f(x) \cdot cos\frac{nπx}{π}dx=\frac{1}{π} ∫_{-π} ^{0}(2x+3)\cdot cos nx dx+\frac{1}{π} ∫_{0} ^{π}(0\cdot cos nx dx=\frac{2}{π} ∫_{-π} ^{0}x\cdot cos nx dx+\frac{3}{π} ∫_{-π} ^{0} cos nx dx=[/m]
Первый интеграл считаем по частям, второй табличный
u=x
dv=cosnx dx
du=dx
v=[m]\frac{1}{n} sinnx[/m]
= решайте
[m]b_{n}=\frac{1}{π} ∫_{-π} ^{π}f(x) \cdot sin\frac{nπx}{π}dx=\frac{1}{π} ∫_{-π} ^{0}(2x+3)\cdot sin nx dx+\frac{1}{π} ∫_{0} ^{π}(0\cdot sin nx dx=\frac{2}{π} ∫_{-π} ^{0}x\cdot sin nx dx+\frac{3}{π} ∫_{-π} ^{0} sin nx dx=[/m]
Первый интеграл считаем по частям, второй табличный
u=x
dv=cosnx dx
du=dx
v=[m]\frac{1}{n} (-cosnx)[/m]
= решайте