Задача 66521 Исследование функции. Исследовать...
Условие
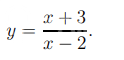
Решение
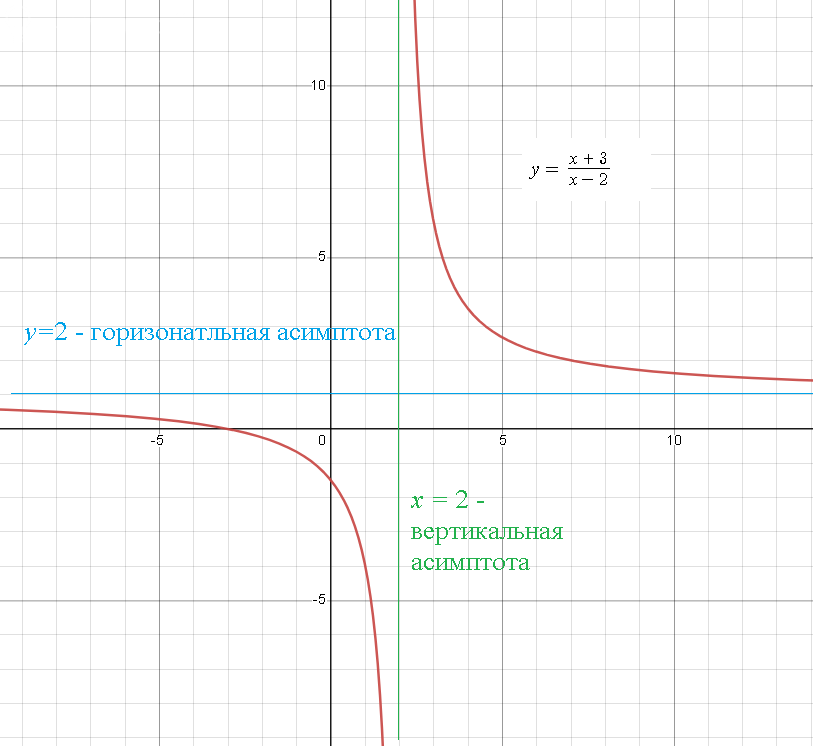
Прямая x=2 - вертикальная асимптота, так как lim_(x → 2)f(x)=lim_(x → 2)(x+3)/(x-2)= ∞
Прямая y=1 - горизонтальная асимптота, так как lim_(x → ∞ )f(x)=lim_(x → ∞ )(x+3)/(x-2)=
Выносим х за скобки и в числителе и в знаменателе и сокращаем на него
=lim_(x → ∞ )x*(1+(3/x))/x*(1-(2/x))=lim_(x → ∞ )(1+(3/x))/(1-(2/x))= 1
Функция не является ни чётной, ни нечётной
y(-x)=((-x)+3)/((-x)-2)=(-x+2)/(-x-2)
y(-x) ≠ y(x) и y(-x) ≠ -y(x)
Находим производную:
y`=((x+3)`·(x-2)–(x+3)·(x-2)`)/(x-2)^2
y`=(1·(x-2)–(x+3)·1)/(x-2)^2
y`=(-5)/(x-2)^2
[b]y` < 0[/b] на (– ∞;2) и на (2;+ ∞ )
Функция убывает на (– ∞;2) и на (2;+ ∞ )
Нет точек экстремума.
y``=5*2/(x-2)^3
y``> 0 на (2;+ ∞ )
на (2;+ ∞ ) кривая выпукла вниз ∪ ( как парабола y=x^2, у которой y``=2 >0)
y``< 0 на (- ∞; 2 )
на (- ∞; 2 ) кривая выпукла вверх ∩ ( как парабола y=-x^2, у которой y``=-2<0)
График см. рис.