Задача 65470 ...
Условие
14) ∑ (2n+1)x^(2n) / n!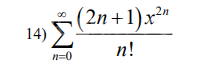
Решение
Например,
[m]e^{x}=1+x+\frac{x^2}{2!}+...+\frac{x^{n}}{n!}+...[/m]
Тогда заменив х на x^2 получим
[m]e^{x^2}=1+x^2+\frac{x^4}{2!}+...+\frac{x^{2n}}{n!}+...[/m]
и понимаем, что правая часть почти похожа на ряд, данный в задаче.
Не хватает множителя (2n+1)
Надо от него избавиться.
Как?
Для этого существуют действия над степенными рядами: дифференцирование и интегрирование..
Понимаем, что
[m] ∫ (2n+1)\frac{x^{2n}}{n!}dx=(2n+1)\frac{1}{n!} ∫ x^{2n}dx=(2n+1)\frac{1}{n!}\cdot \frac{x^{2n+1}}{2n+1}[/m]
Т.е. данный ряд получен дифференцированием ряда
[m] ∑ \frac{x^{2n+1}}{n!}=x\cdot ∑\frac{x^{2n}}{n!} [/m]
теперь ясно, что сумма ряда [b][m]S(x)=x\cdot e^{x^2}[/m][/b]
Все решения
Обычно требуется найти область сходимости ряда или вычислить, какой функции он соответствует.
Я не знаю, как это решать, Вольфрам Альфа показал такую функцию:
[m]y(x) = 2e^{x^2}*x^2 - 3x^2 + e^{x^2} - 1[/m]
Область сходимости можно найти по признаку Даламбера:
Если [m]lim_{n \rightarrow \infty} \frac{a_{n+1}}{a_n} < 1[/m] - тогда ряд сходится.
[m]lim_{n \rightarrow \infty} \frac{(2(n+1) + 1)x^{2(n+1)}}{(n+1)!} : \frac{(2n + 1)x^{2n}}{n!} = lim_{n \rightarrow \infty} \frac{(2n + 3)x^{2n+2}*n!}{(n+1)!*(2n+1)x^{2n}} = [/m]
[m] = lim_{n \rightarrow \infty} \frac{(2n + 3)x^2}{(n+1)(2n+1)} = x^2*lim_{n \rightarrow \infty} \frac{(2n + 3)}{2n^2+3n+1} = 0[/m]
Этот предел равен 0 независимо от x, поэтому область сходимости:
x ∈ (-oo; +oo)