Задача 65463 ...
Условие
Σ (n!)² / (2n)! xⁿ, n=0 to ∞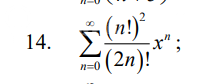
Решение
∑_(n=0)^( ∞) a_(n)x^(n)
[m]a_{n}=\frac{(n!)^2}{(2n)!}[/m]
[m]R=lim_{n → ∞ }\frac{a_{n}}{a_{n+1}}=lim_{n → ∞ }\frac{\frac{(n!)^2}{(2n)!}}{\frac{((n+1)!)^2}{(2(n+1))!}}=lim_{n → ∞ }\frac{(2n+1)(2n+2)}{(n+1)^2}=4[/m]
(-R;R) - интервал сходимости.
Значит
(-4;4) - интервал сходимости данного ряда.
Чтобы указать область сходимости надо проверить сходимость на концах, т.е в точках x=-4 и x=4
При x=4
получаем знакоположительный числовой ряд
∑_(n=0)^( ∞) [m]\frac{(n!)^2}{(2n)!}\cdot 4^{n}[/m]
Признак Даламбера нельзя применить. Получим 1, в этом случае признак ответа не дает.
Стало быть и признак Коши тоже...
Скорее всего признаки Абеля-Дирихле следует применить.
При x=-4
получаем числовой ряд
∑_(n=0)^( ∞) [m]\frac{(n!)^2}{(2n)!}\cdot (-4)^{n}[/m]
∑_(n=0)^( ∞) [m]\frac{(n!)^2}{(2n)!}\cdot (-1)^{n}\cdot 4^{n}[/m] - знакочередующийся ряд.
Признак Лейбница нельзя применить.
Скорее всего признаки Абеля-Дирихле следует применить.