Задача 65391 из угла, тангенс которого равен 7/16,...
Условие
Решение
ВК=17
КС=13
tg ∠ A=7/16
⇒ [b]∠ А - острый.[/b]
Пусть AK=h
∠BAK= α , тогда из прямоугольного треугольника BAK tgα=17/h
∠KAC= β, тогда из прямоугольного треугольника KAC tgβ =13/h
∠ А= α +β
tg ∠ A=7/16
tg( α+β)=(tgα+tgβ)/(1-tgα*tgβ)
7/16= ((17/h)+(13/h))/(1-(17/h)*(13/h))
⇒
7*(1-(221/h^2))=16*(30/h)
⇒ 7-(1547/h^2)=480/h
7h^2-480h-1547=0
D=480^2-4*7*(-1547)=(4*120)^2+4*10829=4*(4*14400+10829)=4*68429
h_(1)=(480+2sqrt(68429))/14; h_(2)=(480-2sqrt(68429))/14<0;
h_(1)=(240+sqrt(68429))/7
S=(1/2)*BC*AK=(1/2)*30*(240+sqrt(68429))/7
S=[b](15/7)*(240+sqrt(68429))[/b]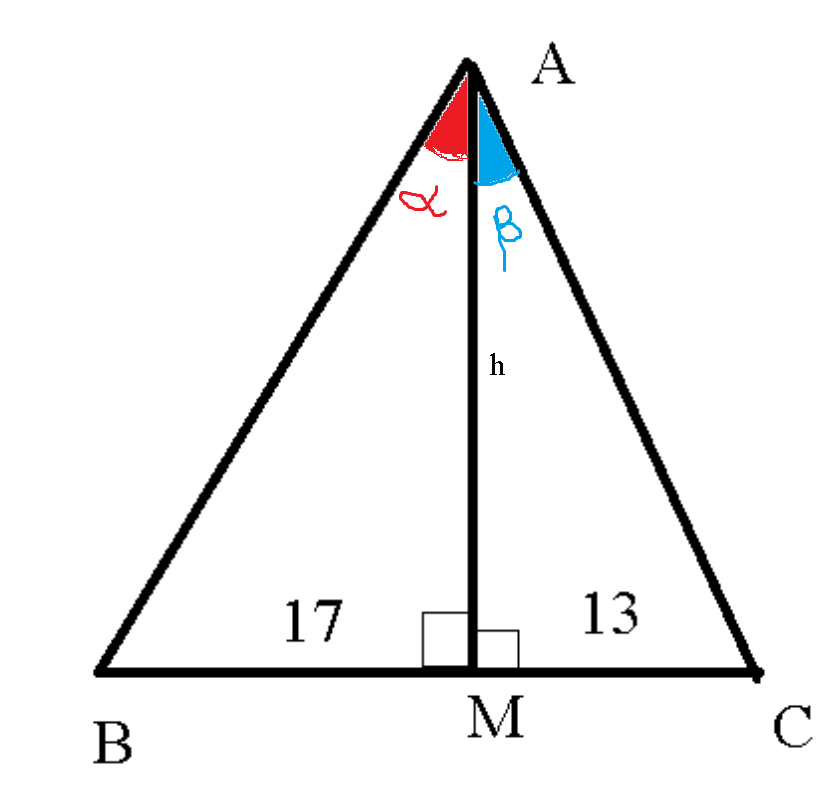
Все решения
Известны только один угол (tg a = 7/16) и одна сторона
(BC = 17 + 13 = 30).
Чтобы определить треугольник однозначно, нужно знать какие-то 3 элемента, одним из которых обязательно должна быть длина (стороны, высоты, медианы, и т.д.).
Значит, или должна быть известна высота AM, или должно быть написано, что треугольник особый - прямоугольный, или равнобедренный, или ещё какой-нибудь.
Без этого найти его площадь невозможно.