Задача 65194 ...
Условие
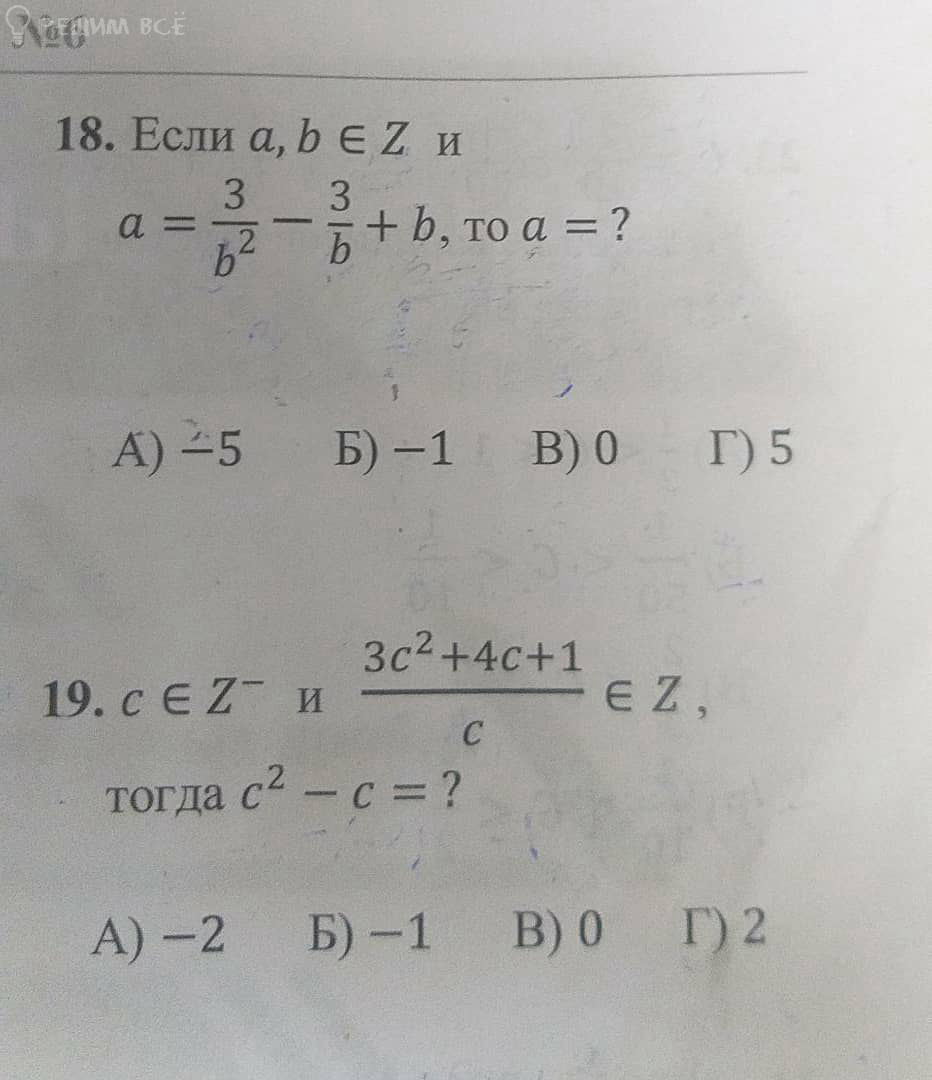
Решение
a ∈ [b]Z[/b]; b ∈[b] Z[/b] ⇒ a-b ∈ [b]Z[/b]
[b]b ≠ 0[/b]
a=(3/b^2)-(3/b)+b ⇒ a-b=(3/b^2)-(3/b) ∈ [b]Z[/b]
3*((1/b^2)-(1/b))∈ [b]Z[/b]
3*(1-b)/b^2∈ [b]Z[/b] ⇒
b^2 делитель числа 3 или b^2 делитель числа (1-b)
делители числа 3: ± 1; ±3
b^2>0
Значит b^2=1 или b^2=3 ( это противоречит тому, что b- целое)
[b]b^2=1 [/b]⇒ b= ± 1
[b]b=1[/b]
3*(1-1)/1=0 ∈ Z ⇒ a=b=1 ( такого ответа нет среди предложенных)
[b]b=-1[/b]
3*(1+1)/(-1)^2=6 ∈ Z ⇒ a-b=6
a=6+b=6+(-1)=5
О т в е т. г) [b]5[/b]
[b]19.[/b]
По условию
с ∈ Z^(-1) - означает, что c - целое отрицательное.
(3c^2 + 4c + 1)/c ∈ Z ⇒ почленно делим на с
(3c^2 + 4c + 1)/c= (3с^2/c) +( 4c/c) +(1/с)=3c+4+(1/c)
3c+4 ∈ Z ⇒ (1/c) ∈ Z
⇒
c= ± 1
Но с ∈ Z^(-1), значит c=-1
с^2-c=(-1)^2-(-1)=[b]2[/b]
О т в е т. г) [b]2[/b]
Все решения
При этом a = 3/b^2 - 3/b + b
b само по себе целое число, значит:
3/b^2 - 3/b - тоже целое число.
Если 3/b - целое, то b - делитель 3, возможны варианты:
1) b = -1; a = 3/b^2 - 3/b + b = 3/1 - 3/(-1) - 1 = 3 + 3 - 1 = 5
2) b = 1; a = 3/b^2 - 3/b + b = 3/1 - 3/1 + 1 = 3 - 3 + 1 = 1
3) b = -3; a = 3/b^2 - 3/b + b = 3/9 - 3/(-3) - 3 - не целое.
4) b = 3; a = 3/b^2 - 3/b + b = 3/9 - 3/3 + 3 - не целое.
Значит, возможные варианты: b = -1; a = 5 или b = 1; a = 1.
Из них нам дан только вариант: Г) 5.
Еще возможен вариант, что дроби 3/b^2 и 3/b - не целые, но их разность - целая.
Однако, повозившись с решением, я получил, что этот вариант тоже невозможен. Поэтому
[b]Ответ: Г) 5[/b]
19) Мы знаем, что числа:
c ∈ Z и (3c^2 + 4c + 1)/c ∈ Z
Надо найти c^2 - c
Выделим в дроби целую часть:
(3c^2 + 4c + 1)/c = 3c + 4 + 1/c ∈ Z
Часть 3c + 4 и так целая, значит, число 1/c - целое.
Возможны варианты:
1) c = -1; c^2 - c = 1 - (-1) = 2
2) c = 1; c^2 - c = 1 - 1 = 0
[b]Ответ: В) 0; Г) 2[/b]